题目内容
14．已知?ABCD的周长为28，自顶点A作AE⊥DC于点E，AF⊥BC于点F．若AE=3，AF=4，则BC=6，CD=8．分析 首先可证得△ADE∽△ABF，又由四边形ABCD是平行四边形，即可求得AB与AD的长．
解答 
解：如图：∵AE⊥DC，AF⊥BC，
∴∠AED=∠AFB=90°，
∵四边形ABCD是平行四边形，
∴∠D=∠B，AB=CD，AD=BC，
∴△ADE∽△ABF，
∴$\frac{AD}{AB}=\frac{AE}{AF}$=$\frac{3}{4}$，
∵AD+CD+BC+AB=28，
即AD+AB=14，
∴AD=6，AB=8，
∴BC=6，AB=8，
故答案为；6，8．
点评 本题考查了平行四边形的性质和相似三角形的性质和判定的应用，关键是正确画出图形，题目比较好，但是有一定的难度．
练习册系列答案
相关题目
如图，抛物线y=ax2+bx+c与x轴的交点坐标是（-2，0），（3，0），则当y＞0时，x的取值范围是x＜-2或x＞3．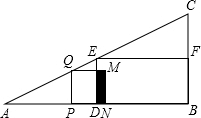
在△ABC中，∠B=90°，AB=12cm，BC=6cm，D、E、F分别为AB、AC边上的中点，若P为AB边上的一个动点，PQ⊥AB，交AC于Q，以PQ为一边，在点A的异侧作正方形PQMN，记正方形PQMN与矩形EDBF的公共部分的面积为y．
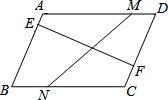如图，四边形ABCD为平行四边形，M，N两点分别从点D到点A、点B到点C运动，速度相同；E，F两点分别从点A到点B，点C到点D运动，速度相同．它们之间用橡皮筋连接．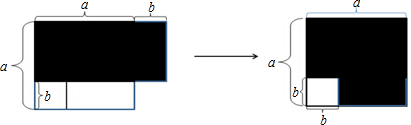
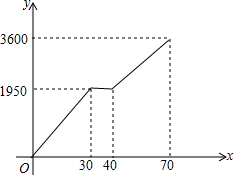小颖和小亮上山游玩，小颖乘坐缆车，小亮步行，两人相约在山顶的缆车终点会合．已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后40分钟后才乘上缆车，缆车的平均速度为180米/分．设小亮出发x分后行走的路程为y米．图中的折线表示小亮在整个行走过程中y随x的变化关系．
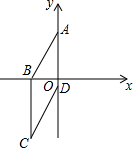四边形ABCD为菱形，已知A（0，4），B（-3，0），求直线OC的解析式．
4．
如图所示，A、B两点的坐标为A（-2，-2），B（4，-2），则C的坐标为（ ）
如图所示，A、B两点的坐标为A（-2，-2），B（4，-2），则C的坐标为（ ）| A． | （2，2） | B． | （0，0） | C． | （0，2） | D． | （4，5） |