题目内容
1.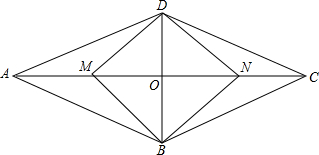 如图,菱形ABCD与矩形BMDN有公共对角线BD,M,N在AC上,且AC=4,BD=2,则AD:DM=$\sqrt{5}$:$\sqrt{2}$.
如图,菱形ABCD与矩形BMDN有公共对角线BD,M,N在AC上,且AC=4,BD=2,则AD:DM=$\sqrt{5}$:$\sqrt{2}$.
分析 由菱形的性质可知BD⊥AC,进而可利用勾股定理分别求出AD,DM的长,则其比值即可求出.
解答 解:∵四边形ABCD是菱形,
∴BD⊥AC,AO=CO,DO=BO,
∴∠AOD=90°,
∵AC=4,BD=2,
∴AO=2,DO=1,
∴AD=$\sqrt{O{D}^{2}+A{O}^{2}}$=$\sqrt{5}$,
∵四边形BMDN是矩形,
∴DB=MN=2,
∴DO=MO=1,
∴DM=$\sqrt{D{O}^{2}+M{O}^{2}}$=$\sqrt{2}$,
∴AD:DM=$\sqrt{5}$:$\sqrt{2}$,
故答案为$\sqrt{5}$:$\sqrt{2}$.
点评 本题考查了菱形的性质、矩形的性质以及勾股定理的运用,解题的关键是充分利用勾股定理求出AD,DM的长,再求它们的比值.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
10.在下列方程中,没有实数根的是( )
| A. | x2+2x-1=0 | B. | x2+2$\sqrt{2}$x+2=0 | C. | x2+$\sqrt{2}$x+1=0 | D. | -x2+2x+2=0 |
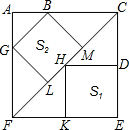 如图,边长为6的大正方形中有两个小正方形,两个小正方形的面积分别为S1、S2
如图,边长为6的大正方形中有两个小正方形,两个小正方形的面积分别为S1、S2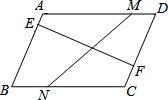 如图,四边形ABCD为平行四边形,M,N两点分别从点D到点A、点B到点C运动,速度相同;E,F两点分别从点A到点B,点C到点D运动,速度相同.它们之间用橡皮筋连接.
如图,四边形ABCD为平行四边形,M,N两点分别从点D到点A、点B到点C运动,速度相同;E,F两点分别从点A到点B,点C到点D运动,速度相同.它们之间用橡皮筋连接.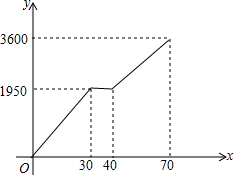 小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后40分钟后才乘上缆车,缆车的平均速度为180米/分.设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后40分钟后才乘上缆车,缆车的平均速度为180米/分.设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.