题目内容
19. 如果正方形网格中的每一个小正方形的边长都是1,则每个小格的顶点叫做格点.
如果正方形网格中的每一个小正方形的边长都是1,则每个小格的顶点叫做格点.(1)如图①,以格点为顶点的△ABC中,请判断AB,BC,AC三边的长度是有理数还是无理数?
(2)在图②中,以格点为顶点画一个三角形,使三角形的三边长分别为3,$\sqrt{5}$,2$\sqrt{2}$.
分析 (1)利用勾股定理得出AB,BC,AC的长,进而得出答案;
(2)直接利用各边长结合勾股定理得出答案.
解答 解:(1)如图①所示:AB=4,AC=$\sqrt{3^2+3^2}$=3$\sqrt{2}$,BC=$\sqrt{1^2+3^2}$=$\sqrt{10}$,
所以AB的长度是有理数,AC和BC的长度是无理数;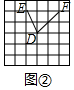
(2)如图②所示:
点评 此题主要考查了勾股定理以及二次根式的应用,正确应用勾股定理是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 如图,其主视图是( )
如图,其主视图是( )
 如图,其主视图是( )
如图,其主视图是( )| A. |  | B. |  | C. |  | D. | 无法确定 |
14.下列四个有理数中,在原点左边的是( )
| A. | -2 014 | B. | 0 | C. | 15.8 | D. | $\frac{1}{2000}$ |
8.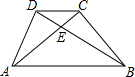 如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE:S△BAE=1:9,则S△DCE:S△BCE为( )
如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE:S△BAE=1:9,则S△DCE:S△BCE为( )
 如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE:S△BAE=1:9,则S△DCE:S△BCE为( )
如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE:S△BAE=1:9,则S△DCE:S△BCE为( )| A. | 1:9 | B. | 1:4 | C. | 1:3 | D. | 9:1 |
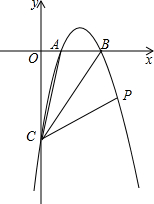 如图,抛物线y=-x2+3x-2与x轴交于A、B两点,与y轴交于C点,点P在抛物线上,∠ACB=∠BCP,求P点的坐标.
如图,抛物线y=-x2+3x-2与x轴交于A、B两点,与y轴交于C点,点P在抛物线上,∠ACB=∠BCP,求P点的坐标.