题目内容
10.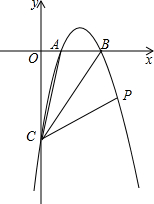 如图,抛物线y=-x2+3x-2与x轴交于A、B两点,与y轴交于C点,点P在抛物线上,∠ACB=∠BCP,求P点的坐标.
如图,抛物线y=-x2+3x-2与x轴交于A、B两点,与y轴交于C点,点P在抛物线上,∠ACB=∠BCP,求P点的坐标.
分析 求出点A关于直线BC 的对称点F′坐标,求出直线CF′的解析式,利用方程组即可求出点P坐标.
解答 解:令y=0,则-x2+3x-2=0,解得x=1或2,
∴点A坐标(1,0),点B坐标(2,0),
令x=0,则y=-2,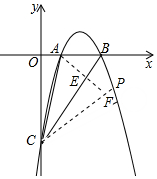
∴点C坐标(0,-2)
设直线BC解析式为y=kx+b,则$\left\{\begin{array}{l}{b=-2}\\{2k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$,
∴直线BC的解析式为y=x-2.
设过点A与直线BC垂直的直线AE的解析式为y=-x+m,(E为垂足),
把A(1,0)代入得到m=1,
∴直线AE的解析式为y=-x+1,
由$\left\{\begin{array}{l}{y=-x+1}\\{y=x-2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$,
则点A关于直线BC的对称点F′(2,-1),
设直线CF′的解析式为y=mx+n,则有$\left\{\begin{array}{l}{n=-2}\\{2m+n=-1}\end{array}\right.$
解得$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=-2}\end{array}\right.$,
∴直线CF′的解析式为y=$\frac{1}{2}$x-2,设直线CF′与抛物线交于点P,
根据对称性可知∠PCB=∠ACB,
由$\left\{\begin{array}{l}{y=\frac{1}{2}x-2}\\{y=-{x}^{2}+3x-2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=0}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=-\frac{3}{4}}\end{array}\right.$,
∴点P坐标为($\frac{5}{2}$,-$\frac{3}{4}$).
点评 本题考查抛物线与x轴的交点、二次函数的性质等知识,解题的关键是取特殊点解决问题,学会利用方程组求两个函数交点坐标,属于中考常考题型.

 如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形),则$\frac{y}{x}$的值为( )
如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形),则$\frac{y}{x}$的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\sqrt{5}$-1 | D. | $\sqrt{5}$+1 |
| A. | -4 | B. | 4 | C. | 2 | D. | -2 |
| A. | 底与边不相等的等腰三角形 | B. | 等边三角形 | ||
| C. | 钝角三角形 | D. | 直角三角形 |
 如果正方形网格中的每一个小正方形的边长都是1,则每个小格的顶点叫做格点.
如果正方形网格中的每一个小正方形的边长都是1,则每个小格的顶点叫做格点.