题目内容
8．
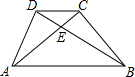如图，梯形ABCD中，AB∥CD，AC、BD交于E，若S△DCE：S△BAE=1：9，则S△DCE：S△BCE为（ ）| A． | 1：9 | B． | 1：4 | C． | 1：3 | D． | 9：1 |
分析 由相似三角形的性质可求得DE：BE，再利用同高三角形的面积比等于底的比，可求得答案．
解答 解：
∵AB∥CD，
∴△DCE∽△BAE，
∴$\frac{{S}_{△DCE}}{{S}_{△BAE}}$=（$\frac{DE}{BE}$）2=$\frac{1}{9}$，
∴DE：BE=1：3，
∵△DCE和△BCE是同高三角形，
∴S△DCE：S△BCE=DE：BE=1：3，
故选C．
点评 本题主要考查相似三角形的判定和性质，由条件求得DE：BE是解题的关键，注意同高三角形的面积比等于其底的比．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
18．
如图，将正方形沿图中虚线（其中x＜y）剪成①②③④四块图形，用这四块图形恰能拼成一个矩形（非正方形），则$\frac{y}{x}$的值为（ ）
如图，将正方形沿图中虚线（其中x＜y）剪成①②③④四块图形，用这四块图形恰能拼成一个矩形（非正方形），则$\frac{y}{x}$的值为（ ）| A． | $\frac{\sqrt{5}-1}{2}$ | B． | $\frac{\sqrt{5}+1}{2}$ | C． | $\sqrt{5}$-1 | D． | $\sqrt{5}$+1 |
如果正方形网格中的每一个小正方形的边长都是1，则每个小格的顶点叫做格点．
20．已知a、b、c是三角形的三边长，如果满足（a-6）2+|b-8|+$\sqrt{c-10}$=0，则三角形的形状是（ ）
| A． | 底与边不相等的等腰三角形 | B． | 等边三角形 | ||
| C． | 钝角三角形 | D． | 直角三角形 |