题目内容
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,过B点作BC的垂线与过A点作AB的垂线交于点E,延长BA于点D,使得DE⊥CD,连接CE交BD于F,已知AD=3,则EF=
如图,在Rt△ABC中,∠ACB=90°,AC=BC,过B点作BC的垂线与过A点作AB的垂线交于点E,延长BA于点D,使得DE⊥CD,连接CE交BD于F,已知AD=3,则EF=考点:勾股定理,等腰直角三角形,相似三角形的判定与性质
专题:
分析:先证明△ACB、△EAB与△CDE都是等腰直角三角形,再设AC=BC=x,则AB=AE=
x,BE=2x,CE=
x,DE=
x,在Rt△ADE中利用勾股定理列出关于x的方程,解方程求出x的值,再由△BEF∽△ACF,得出EF=2CF,进而求出EF的值.
| 2 |
| 5 |
| ||
|
解答: 解:∵在Rt△ABC中,∠ACB=90°,AC=BC,
解:∵在Rt△ABC中,∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,∠ABC=45°.
∵BE⊥BC,
∴∠EBC=90°,∠ABE=90°-∠ABC=45°,
又∵EA⊥AB,
∴△EAB是等腰直角三角形,AB=AE,∠ABE=45°.
∵∠CDE+∠EBC=90°+90°=180°,
∴B、C、D、E四点共圆,
∴∠DCE=∠DBE=45°,
∴△CDE是等腰直角三角形.
设AC=BC=x,则AB=AE=
x,BE=
AB=2x,CE=
=
x,DE=
=
x.
在Rt△ADE中,∵∠DAE=90°,
∴DE2=AD2+AE2,即(
x)2=32+(
x)2,
化简整理,得
x2=9,解得x=±3
(负值舍去),
∴CE=
x=3
.
∵BE⊥BC,AC⊥BC,
∴BE∥AC,
∴△BEF∽△ACF,
∴
=
=
=2,
∴EF=2CF,
∴EF=
CE=2
.
故答案为:2
.
 解:∵在Rt△ABC中,∠ACB=90°,AC=BC,
解:∵在Rt△ABC中,∠ACB=90°,AC=BC,∴△ABC是等腰直角三角形,∠ABC=45°.
∵BE⊥BC,
∴∠EBC=90°,∠ABE=90°-∠ABC=45°,
又∵EA⊥AB,
∴△EAB是等腰直角三角形,AB=AE,∠ABE=45°.
∵∠CDE+∠EBC=90°+90°=180°,
∴B、C、D、E四点共圆,
∴∠DCE=∠DBE=45°,
∴△CDE是等腰直角三角形.
设AC=BC=x,则AB=AE=
| 2 |
| 2 |
| BE2+BC2 |
| 5 |
| CE | ||
|
| ||
|
在Rt△ADE中,∵∠DAE=90°,
∴DE2=AD2+AE2,即(
| ||
|
| 2 |
化简整理,得
| 1 |
| 2 |
| 2 |
∴CE=
| 5 |
| 10 |
∵BE⊥BC,AC⊥BC,
∴BE∥AC,
∴△BEF∽△ACF,
∴
| EF |
| CF |
| BE |
| AC |
| 2x |
| x |
∴EF=2CF,
∴EF=
| 2 |
| 3 |
| 10 |
故答案为:2
| 10 |
点评:本题主要考查了等腰直角三角形、相似三角形的判定与性质,勾股定理,四点共圆,有一定难度.设出适当的未知数x,在Rt△ADE中利用勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
 由一个圆柱体与一个长方体组成的几何体如图,这个几何体的左视图是( )
由一个圆柱体与一个长方体组成的几何体如图,这个几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
下列运算中正确的是( )
| A、(-ab)2=2a2b2 |
| B、(a+1)2=a2+1 |
| C、a6÷a2=a3 |
| D、(-x2)3=-x6 |
 如图,在四边形ABCD中,若AD∥BC,BC=CD=AC=6,AB=3
如图,在四边形ABCD中,若AD∥BC,BC=CD=AC=6,AB=3 如图,MN是⊙O的直径,矩形ABCD的顶点A、D在MN上,顶点B、C在⊙O上,若⊙O的半径为5,AB=4,则AD边的长为
如图,MN是⊙O的直径,矩形ABCD的顶点A、D在MN上,顶点B、C在⊙O上,若⊙O的半径为5,AB=4,则AD边的长为 如图,⊙0的半径OD上弦AB于点C,若AB=8,CD=2,则⊙0的半径为
如图,⊙0的半径OD上弦AB于点C,若AB=8,CD=2,则⊙0的半径为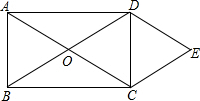 如图,矩形ABCD中,对角线AC、BD交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD中,对角线AC、BD交于点O,DE∥AC,CE∥BD.