题目内容
8. 如图,在?ABCD中,DF⊥AB于F,DE⊥BC于E,
如图,在?ABCD中,DF⊥AB于F,DE⊥BC于E,(1)∠A=40°,求∠FDE的度数;
(2)若DE=4,DF=6.?ABCD的周长为40,求S?ABCD.
分析 (1)根据平行四边形性质求出∠B,在四边形DFBE中,利用∠EDF+∠B=180°解决.
(2)设AB=x,BC=y列出方程组求出x、y,再代入平行四边形面积公式即可.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A=40°,
∴∠B=140°,
在四边形DFBE中,∵DF⊥AB,DE⊥BC,
∴∠DFB=∠DEB=90°,
∴∠EDF+∠B=180°,
∴∠EDF=40°.
(2)设AB=x,BC=y,由题意$\left\{\begin{array}{l}{x+y=20}\\{6x=4y}\end{array}\right.$解得$\left\{\begin{array}{l}{x=8}\\{y=12}\end{array}\right.$,
∴S平行四边形ABCD=6×8=48.
点评 本题考查平行四边形性质、勾股定理以及平行四边形面积公式,设未知数列出方程组是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.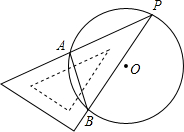 如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A、B两点,若⊙O的直径为4,则弦AB长为( )
如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A、B两点,若⊙O的直径为4,则弦AB长为( )
 如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A、B两点,若⊙O的直径为4,则弦AB长为( )
如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A、B两点,若⊙O的直径为4,则弦AB长为( )| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 如图,在?ABCD中,AC⊥AB,若BC=10cm,AC=8cm,则AB=6cm,DC=6cm,AD=10cm.
如图,在?ABCD中,AC⊥AB,若BC=10cm,AC=8cm,则AB=6cm,DC=6cm,AD=10cm. 已知图中小方格的边长为1,求点C到线段AB的距离.
已知图中小方格的边长为1,求点C到线段AB的距离. 如图,DE+AB=AD,∠1=∠E.求证:
如图,DE+AB=AD,∠1=∠E.求证:
 如图,在?ABCD中,E为BC上的一点,且AE与DE分别平分∠BAD和∠ADC
如图,在?ABCD中,E为BC上的一点,且AE与DE分别平分∠BAD和∠ADC 如图所示,BE=CF,BF⊥AC于点F,CE⊥AB于点E,BF和CE交于点D,求证:AD平分∠BAC.
如图所示,BE=CF,BF⊥AC于点F,CE⊥AB于点E,BF和CE交于点D,求证:AD平分∠BAC.