题目内容
16. 已知图中小方格的边长为1,求点C到线段AB的距离.
已知图中小方格的边长为1,求点C到线段AB的距离.
分析 连接AC,AB,根据勾股定理可求得三角形各边的长,从而得到该三角形是等腰三角形,根据等腰三角形三线合一的性质可求得底边AC上的高,再根据面积公式求得AB边上的高即可.
解答  解:连接AC,BC.如图所示:
解:连接AC,BC.如图所示:
根据勾股定理求得:AC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,BC=AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∴△ABC是等腰三角形,
∴AC上的高=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴该三角形的面积=$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{2}$=4,
∴AB边上的高=$\frac{4×2}{\sqrt{10}}$=$\frac{4}{5}$$\sqrt{10}$,
即点C到线段AB的距离我$\frac{4}{5}$$\sqrt{10}$.
点评 本题考查了勾股定理、三角形面积的计算;熟练掌握勾股定理,由三角形的面积的计算方法得出结果是解决问题的关键.

练习册系列答案
相关题目
11. 为了解某校九年级学生中考体育测试成绩,现从中随机抽取部分学生的中考体育成绩进行分段(A等:90~100分;B等:75~89分;C等:60~74分;D等:60分以下)统计如下:
为了解某校九年级学生中考体育测试成绩,现从中随机抽取部分学生的中考体育成绩进行分段(A等:90~100分;B等:75~89分;C等:60~74分;D等:60分以下)统计如下:
请你根据以上图表提供的信息,解答下列问题:
(1)x=0.38,n=8;
(2)在扇形统计图中,B等级所对应的扇形圆心角是144度;
(3)如果把成绩在60分以上(含60分)定为合格,若该校九年级共有500名学生参加了本次中考体育测试,那么请你估计成绩为合格的学生人数约有多少名?
 为了解某校九年级学生中考体育测试成绩,现从中随机抽取部分学生的中考体育成绩进行分段(A等:90~100分;B等:75~89分;C等:60~74分;D等:60分以下)统计如下:
为了解某校九年级学生中考体育测试成绩,现从中随机抽取部分学生的中考体育成绩进行分段(A等:90~100分;B等:75~89分;C等:60~74分;D等:60分以下)统计如下:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 90~100 | 19 | x |
| B | 75~89 | 20 | 0.4 |
| C | 60~74 | n | 0.16 |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(1)x=0.38,n=8;
(2)在扇形统计图中,B等级所对应的扇形圆心角是144度;
(3)如果把成绩在60分以上(含60分)定为合格,若该校九年级共有500名学生参加了本次中考体育测试,那么请你估计成绩为合格的学生人数约有多少名?
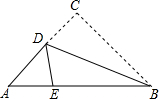 如图的三角形纸片中,AB=8cm,BC=6cm,AC=7cm,沿过点B的直线折叠三角形,使点C落在AB边的点E处,折痕为BD,则△AED的周长为9cm.
如图的三角形纸片中,AB=8cm,BC=6cm,AC=7cm,沿过点B的直线折叠三角形,使点C落在AB边的点E处,折痕为BD,则△AED的周长为9cm.
 如图,在?ABCD中,DF⊥AB于F,DE⊥BC于E,
如图,在?ABCD中,DF⊥AB于F,DE⊥BC于E, 已知抛物线y=ax2+bx+c(a<0)经过点A(-3,0)、B(1,0),且与y轴交于点C,设抛物线的顶点为D.
已知抛物线y=ax2+bx+c(a<0)经过点A(-3,0)、B(1,0),且与y轴交于点C,设抛物线的顶点为D. 已知:如图,△ABC、△CDE、△EHK都是等边三角形,且A、D、K共线,AD=DK,求证:△HBD也是等边三角形.
已知:如图,△ABC、△CDE、△EHK都是等边三角形,且A、D、K共线,AD=DK,求证:△HBD也是等边三角形.