题目内容
10. 如图,在?ABCD中,E为BC上的一点,且AE与DE分别平分∠BAD和∠ADC
如图,在?ABCD中,E为BC上的一点,且AE与DE分别平分∠BAD和∠ADC(1)求证:AE⊥DE;
(2)设以AD为直径的半圆交AB于F,DF交AE于G,已知CD=5,AE=8,求tan∠BAE的值.
分析 (1)根据是ABCD平行四边形,得出AB∥CD,则∠BAD+∠ADC=180°,又根据AE、DE是∠BAD、∠ADC的角平分线,得出∠DAE+∠ADE=90°,即可得出AE⊥DE;
(2)由于AD∥BC,AE是角平分线,容易得∠BAE=∠BEA,那么AB=BE=CD=5,同理有CE=CD=5,容易得出AD=BC=BE+CE=10,在Rt△ADE中,利用勾股定理可求DE,由于AD是直径,所以tan∠FAG=$\frac{FG}{AF}$,而∠FAG=∠DAE,于是$\frac{FG}{AF}$=$\frac{DE}{AE}$,即可求解.
解答 解:(1)证明:在平行四边形ABCD中,AB∥CD,
∴∠BAD+∠ADC=180°.
又∵AE、DE平分∠BAD、∠ADC,
∴∠DAE+∠ADE=90°,
∴∠AED=90°,
∴AE⊥DE.
(2)在平行四边形ABCD中,AD∥BC,AB=CD=5,AD=BC,
∴∠DAE=∠BEA.
又∵∠DAE=∠BAE,
∴∠BEA=∠BAE,
∴BE=AB=5.
同理EC=CD=5.
∴AD=BC=BE+EC=10.
在Rt△AED中,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6.
又∵AE是∠BAD的角平分线,
∴∠FAG=∠DAE.
∵AD是直径,
∴∠AFD=90°,
∴tan∠FAG=$\frac{FG}{AF}$,
∴$\frac{FG}{AF}$=tan∠DAE=$\frac{DE}{AE}$=$\frac{6}{8}$=$\frac{3}{4}$,
∴tan∠BAE=$\frac{3}{4}$.
点评 本题考查了相似三角形的判定和性质,勾股定理,平行四边形的性质,角平分线的定义,熟练掌握各定理是解题的关键.

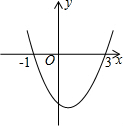 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:①a>0;②b>0;③a+b+c>0;④2a+b=0;⑤方程ax2+bx+c=0的解为x1=-1,x2=3.
其中正确的是( )
| A. | ①②③ | B. | ②③④ | C. | ③④⑤ | D. | ①④⑤ |
 为了解某校九年级学生中考体育测试成绩,现从中随机抽取部分学生的中考体育成绩进行分段(A等:90~100分;B等:75~89分;C等:60~74分;D等:60分以下)统计如下:
为了解某校九年级学生中考体育测试成绩,现从中随机抽取部分学生的中考体育成绩进行分段(A等:90~100分;B等:75~89分;C等:60~74分;D等:60分以下)统计如下:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 90~100 | 19 | x |
| B | 75~89 | 20 | 0.4 |
| C | 60~74 | n | 0.16 |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(1)x=0.38,n=8;
(2)在扇形统计图中,B等级所对应的扇形圆心角是144度;
(3)如果把成绩在60分以上(含60分)定为合格,若该校九年级共有500名学生参加了本次中考体育测试,那么请你估计成绩为合格的学生人数约有多少名?
 如图,在?ABCD中,DF⊥AB于F,DE⊥BC于E,
如图,在?ABCD中,DF⊥AB于F,DE⊥BC于E,
 已知抛物线y=ax2+bx+c(a<0)经过点A(-3,0)、B(1,0),且与y轴交于点C,设抛物线的顶点为D.
已知抛物线y=ax2+bx+c(a<0)经过点A(-3,0)、B(1,0),且与y轴交于点C,设抛物线的顶点为D. 如图,点A,B,C,D在同一直线上,AB=CD,AE∥CF且AE=CF,求证:BE=DF.
如图,点A,B,C,D在同一直线上,AB=CD,AE∥CF且AE=CF,求证:BE=DF.
