题目内容
19. 如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,求BC的长.
如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,求BC的长.
分析 先求出∠ABC=60°,再求出∠CBD=∠ABD=30°,得出∠ABD=∠A,求出BD,再求出CD,最后根据BC=$\sqrt{B{D}^{2}-C{D}^{2}}$代入计算即可.
解答 解:∵∠C=90°,∠A=30°,
∴∠ABC=60°,
∵BD是∠ABC的平分线,
∴∠CBD=∠ABD=30°,
∴∠ABD=∠A,
∴AD=BD=20,
∴CD=$\frac{1}{2}$BD=10,
∴BC=$\sqrt{B{D}^{2}-C{D}^{2}}$=$\sqrt{2{0}^{2}-1{0}^{2}}$=10$\sqrt{3}$.
点评 本题考查了含30°角的直角三角形,用到的知识点是角平分线的性质、等腰三角形的性质、勾股定理,解题的关键是得出BD=AD.

练习册系列答案
相关题目
7. 如图,在?ABCD中,它的周长是36cm.AB=8cm,则BC等于( )
如图,在?ABCD中,它的周长是36cm.AB=8cm,则BC等于( )
 如图,在?ABCD中,它的周长是36cm.AB=8cm,则BC等于( )
如图,在?ABCD中,它的周长是36cm.AB=8cm,则BC等于( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 14cm |
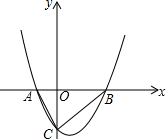 已知抛物线y=ax2-2ax+n(a>0)与x轴交于A(x1,0),B(x2,0).交y轴的负半轴于点C,且x1<x2,OC=OB,S△ABC=6.
已知抛物线y=ax2-2ax+n(a>0)与x轴交于A(x1,0),B(x2,0).交y轴的负半轴于点C,且x1<x2,OC=OB,S△ABC=6.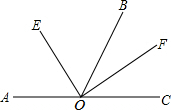 如图,AC为一条直线,O是AC上一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC.
如图,AC为一条直线,O是AC上一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC.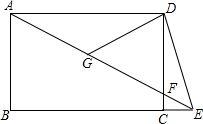 如图,四边形ABCD是矩形,点E在线段BC的延长线上,连接AE交CD于点F,∠AED=2∠AEB,点G是AF的中点.若CE=1,AG=3,则AB的长为2$\sqrt{2}$.
如图,四边形ABCD是矩形,点E在线段BC的延长线上,连接AE交CD于点F,∠AED=2∠AEB,点G是AF的中点.若CE=1,AG=3,则AB的长为2$\sqrt{2}$.