题目内容
5.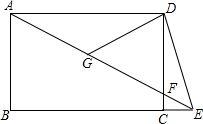 如图,四边形ABCD是矩形,点E在线段BC的延长线上,连接AE交CD于点F,∠AED=2∠AEB,点G是AF的中点.若CE=1,AG=3,则AB的长为2$\sqrt{2}$.
如图,四边形ABCD是矩形,点E在线段BC的延长线上,连接AE交CD于点F,∠AED=2∠AEB,点G是AF的中点.若CE=1,AG=3,则AB的长为2$\sqrt{2}$.
分析 根据直角三角形斜边上的中线等于斜边的一半可得AG=DG,然后根据等边对等角的性质可得∠ADG=∠DAG,再结合两直线平行,内错角相等可得∠ADG=∠AEB,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠DGE=2∠ADG,从而得到∠DEG=∠DGE,再利用等角对等边的性质得到DE=DG,然后利用勾股定理列式计算即可得解.
解答 解:∵四边形ABCD是矩形,点G是DF的中点,
∴AG=DG,
∴∠ADG=∠DAG,
∵AD∥BC,
∴∠ADG=∠AEB,
∴∠DGE=∠ADG+∠DAG=2∠AEB,
∵∠AED=2∠AEB,
∴∠DEG=∠DGE,
∴DE=DG=AG=3,
在Rt△CDE中,CD=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$.
∴AB=CD=2$\sqrt{2}$.
点评 本题考查了矩形的性质,等边对等角的性质,等角对等边的性质,以及勾股定理的应用,求出DE=AG是解题的关键.

练习册系列答案
相关题目
10.在平面直角坐标系中,点A(0,2),在x轴上任取一点M,连接AM,作AM的垂直平分线l1,过点M作x轴的垂线
l2.l1与l2交于点P.设P点的坐标为(x,y),那么x,y满足的关系式为( )
l2.l1与l2交于点P.设P点的坐标为(x,y),那么x,y满足的关系式为( )
| A. | y=$\frac{{x}^{2}}{4}$+1 | B. | y=x2+2x+1 | C. | y=2x2+1 | D. | y=x2+1 |
17. 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是(用含a、b的式子表示)( )
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是(用含a、b的式子表示)( )
 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是(用含a、b的式子表示)( )
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是(用含a、b的式子表示)( )| A. | (a+b)2 | B. | (a-b)2 | C. | 2ab | D. | ab |
14.二次函数y=2(x+3)2-1的图象的顶点所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15. 由如图通过平移后可以得到的图案是( )
由如图通过平移后可以得到的图案是( )
 由如图通过平移后可以得到的图案是( )
由如图通过平移后可以得到的图案是( )| A. |  | B. |  | C. |  | D. |  |
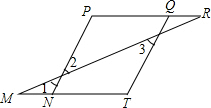 (1)如图,点M、N、T和点P、Q、R分别在同一条直线上,且∠1=∠3,∠P=∠T,求证:∠MTQ=∠RQT.
(1)如图,点M、N、T和点P、Q、R分别在同一条直线上,且∠1=∠3,∠P=∠T,求证:∠MTQ=∠RQT. 如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,求BC的长.
如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,求BC的长. 已知,BE,DE分别平分∠ABD,∠CDB,BE⊥DE,求证:AB∥CD.
已知,BE,DE分别平分∠ABD,∠CDB,BE⊥DE,求证:AB∥CD. 如图所示,AD⊥BC于点D,EG交B于点G,∠E=∠1,若AD平分∠BAC,试判断是否EG⊥BC,请说明理由.
如图所示,AD⊥BC于点D,EG交B于点G,∠E=∠1,若AD平分∠BAC,试判断是否EG⊥BC,请说明理由.