题目内容
4.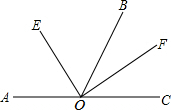 如图,AC为一条直线,O是AC上一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC.
如图,AC为一条直线,O是AC上一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC.(1)求∠EOF的大小;
(2)当OB绕O旋转时,OE,OF仍为∠AOB和∠BOC的平分线,问:OE,OF有怎样的位置关系?你能否用一句话概括出这个结论?
分析 (1)先由点O是AC上一点,得出∠AOB+∠BOC=∠AOC=180°,再由OE,OF分别平分∠AOB,∠BOC,根据角平分线定义得出∠BOE=$\frac{1}{2}$∠AOB,∠BOF=$\frac{1}{2}$∠BOC,那么∠EOF=∠BOE+∠BOF=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠BOC=$\frac{1}{2}$∠AOC=90°;
(2)当OB绕O点旋转时,若OE,OF仍为∠AOB和∠BOC的平分线,仍然可以得到∠EOF=90°,根据垂直的定义得出OE⊥OF.
解答 解:(1)∵点O是AC上一点,
∴∠AOB+∠BOC=∠AOC=180°,
∵OE,OF分别平分∠AOB,∠BOC,
∴∠BOE=$\frac{1}{2}$∠AOB,∠BOF=$\frac{1}{2}$∠BOC,
∴∠EOF=∠BOE+∠BOF
=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠BOC
=$\frac{1}{2}$∠AOC
=90°;
(2)当OB绕O旋转时,
∵点O是AC上一点,
∴∠AOB+∠BOC=∠AOC=180°,
∵OE,OF分别平分∠AOB,∠BOC,
∴∠BOE=$\frac{1}{2}$∠AOB,∠BOF=$\frac{1}{2}$∠BOC,
∴∠EOF=∠BOE+∠BOF
=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠BOC
=$\frac{1}{2}$∠AOC
=90°,
∴OE⊥OF.
由此得到:邻补角的两角的平分线互相垂直.
点评 此题综合考查角平分线,余角,要记住互为余角的两个角的和为90度.同时考查了垂直的判定.

练习册系列答案
相关题目
10.在平面直角坐标系中,点A(0,2),在x轴上任取一点M,连接AM,作AM的垂直平分线l1,过点M作x轴的垂线
l2.l1与l2交于点P.设P点的坐标为(x,y),那么x,y满足的关系式为( )
l2.l1与l2交于点P.设P点的坐标为(x,y),那么x,y满足的关系式为( )
| A. | y=$\frac{{x}^{2}}{4}$+1 | B. | y=x2+2x+1 | C. | y=2x2+1 | D. | y=x2+1 |
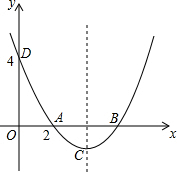 如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A的坐标为(2,0),与y轴的交点为D(0,4),抛物线的对称轴为直线x=3.
如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A的坐标为(2,0),与y轴的交点为D(0,4),抛物线的对称轴为直线x=3. 如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,求BC的长.
如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,求BC的长. 已知,BE,DE分别平分∠ABD,∠CDB,BE⊥DE,求证:AB∥CD.
已知,BE,DE分别平分∠ABD,∠CDB,BE⊥DE,求证:AB∥CD.