题目内容
12.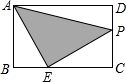 如图,在矩形ABCD中,AB=2,AD=3,BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是
如图,在矩形ABCD中,AB=2,AD=3,BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )
| A. |  | B. | 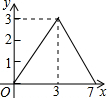 | C. | 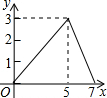 | D. |  |
分析 求出CE的长,然后分①点P在AD上时,利用三角形的面积公式列式得到y与x的函数关系;②点P在CD上时,根据S△APE=S梯形AECD-S△ADP-S△CEP列式整理得到y与x的关系式;③点P在CE上时,利用三角形的面积公式列式得到y与x的关系式,然后选择答案即可.
解答 解:∵在矩形ABCD中,AB=2,AD=3,
∴CD=AB=2,BC=AD=3,
∵BE=1,
∴CE=BC-BE=2,
①点P在AD上时,△APE的面积y=$\frac{1}{2}$x•2=x(0≤x≤3),
②点P在CD上时,S△APE=S梯形AECD-S△ADP-S△CEP,
=$\frac{1}{2}$(2+3)×2-$\frac{1}{2}$×3×(x-3)-$\frac{1}{2}$×2×(3+2-x),
=5-$\frac{3}{2}$x+$\frac{9}{2}$-5+x,
=-$\frac{1}{2}$x+$\frac{9}{2}$,
∴y=-$\frac{1}{2}$x+$\frac{9}{2}$(3<x≤5),
③点P在CE上时,S△APE=$\frac{1}{2}$×(3+2+2-x)×2=-x+7,
∴y=-x+7(5<x≤7),
故选:A.
点评 本题考查了动点问题函数图象,读懂题目信息,根据点P的位置的不同分三段列式求出y与x的关系式是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
2.解关于x的方程$\frac{x-6}{x-2}$=$\frac{a}{x-2}$产生增根,则常数a的值等于( )
| A. | 2 | B. | -3 | C. | -4 | D. | -5 |
3.下列计算正确的是( )
| A. | a3•a2=a6 | B. | 6a2÷2a2=3a2 | C. | x5+x5=x10 | D. | y7•y=y8 |
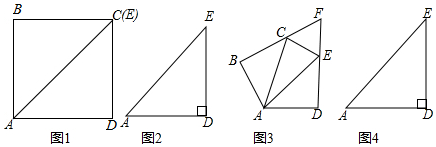
 如图,请填写一个使AB∥CD的条件∠BAE=∠ADC(答案不唯一).
如图,请填写一个使AB∥CD的条件∠BAE=∠ADC(答案不唯一).