题目内容
17．解不等式组$\left\{\begin{array}{l}{2x+5≤3（x+2）①}\\{\frac{1-2x}{3}+\frac{1}{5}＞0②}\end{array}\right.$，并把解集表示在数轴上．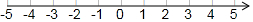
分析 先求出每个不等式的解集，再求出不等式组的解集即可．
解答 解：∵解不等式①得：x≥-1，
解不等式②得：x＜0.8，
∴不等式组的解集为-1≤x＜0.8，
在数轴上表示为：
．
点评 本题考查了解一元一次不等式组和在数轴上表示不等式组的解集，能根据不等式的解集求出不等式组的解集是解此题的关键．
练习册系列答案
金钥匙试卷系列答案
相关题目
7．在?ABCD中，∠B=2∠A，则∠B的度数为（ ）
| A． | 30° | B． | 60° | C． | 90° | D． | 120° |
8．下列四个图形中，是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
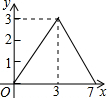
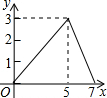
如图，△ABC中，∠B=∠C，点D，E分别是BC，AC的中点，若AC=6，则DE的长为3．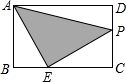
如图，在矩形ABCD中，AB=2，AD=3，BE=1，动点P从点A出发，沿路径A→D→C→E运动，则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是
9．在下列所给出的坐标中，所表示的点在第一象限的是（ ）
| A． | （2，3） | B． | （-2，3） | C． | （-2，-3） | D． | （2，-3） |
7．
如图，已知∠ABC=∠DCB，添加下列条件，△ABC与△DCB不能全等是（ ）
如图，已知∠ABC=∠DCB，添加下列条件，△ABC与△DCB不能全等是（ ）| A． | AC=DB | B． | AB=DC | C． | ∠A=∠D | D． | ∠1=∠2 |