题目内容
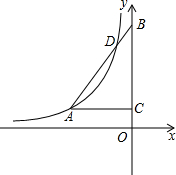 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,B、C均在y轴上,且B点坐标为(0,4
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,B、C均在y轴上,且B点坐标为(0,4| 3 |
| k |
| x |
| A、-3 | ||
B、-3
| ||
C、-2
| ||
D、-4
|
考点:反比例函数综合题
专题:
分析:过点D作DE⊥AC于点E,过点D作DF⊥BC于点F,设点A的坐标为(a,b),点D的坐标为(c,d),在Rt△AED中运用三角函数的定义可以得到a、b、c、d一个等量关系,易证△BFD∽△BCA,运用相似三角形的性质可得a=3c,由点A、D在反比例函数y=
的图象上可得k=ab=cd,从而得到d=3b,进而可得b=-
a,在Rt△ACB中,运用三角函数的定义可得BC=-
a,由B点坐标为(0,4
)可得OB=4
,由此可求出a的值,从而求出b的值,进而求出k的值,问题得以解决.
| k |
| x |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
解答: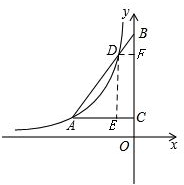 解:过点D作DE⊥AC于点E,过点D作DF⊥BC于点F,如图.
解:过点D作DE⊥AC于点E,过点D作DF⊥BC于点F,如图.
设点A的坐标为(a,b),点D的坐标为(c,d),
则有AC=-a,OC=b,DF=-c,OF=d,
∴AE=AC-CE=AC-DF=-a-(-c)=-a+c,DE=FC=OF-OC=d-b.
∵∠ACB=90°,∠ABC=30°,∴∠BAC=60°.
∴在Rt△AED中,DE=AE•tan∠DAE=
AE,
则d-b=
(-a+c).
∵DE⊥AC,∠ACB=90°,
∴∠BFD=∠ACB=90°,
∵∠DBF=∠ABC,
∴△BFD∽△BCA,
∴
=
.
∵AD=2BD,∴
=
=
,
∴AC=3DF,
∴-a=-3c,即c=
a.
∵点A、D在反比例函数y=
的图象上,
∴k=ab=cd,∴d=3b.
∵d-b=
(-a+c),
∴2b=
(-a+
a)=-
a,
∴b=-
a.
在Rt△ACB中,
∵∠BAC=60°,∴BC=AC•tan∠BAC=-
a.
∵B点坐标为(0,4
),∴OB=4
,
∴OB=BC+OC=-
a+b=-
a+(-
a)=-
a=4
,
∴a=-3.
∴b=-
a=
,
∴k=ab=-3×
=-3
.
故选:B.
 解:过点D作DE⊥AC于点E,过点D作DF⊥BC于点F,如图.
解:过点D作DE⊥AC于点E,过点D作DF⊥BC于点F,如图.设点A的坐标为(a,b),点D的坐标为(c,d),
则有AC=-a,OC=b,DF=-c,OF=d,
∴AE=AC-CE=AC-DF=-a-(-c)=-a+c,DE=FC=OF-OC=d-b.
∵∠ACB=90°,∠ABC=30°,∴∠BAC=60°.
∴在Rt△AED中,DE=AE•tan∠DAE=
| 3 |
则d-b=
| 3 |
∵DE⊥AC,∠ACB=90°,
∴∠BFD=∠ACB=90°,
∵∠DBF=∠ABC,
∴△BFD∽△BCA,
∴
| DF |
| AC |
| BD |
| AB |
∵AD=2BD,∴
| DF |
| AC |
| BD |
| AB |
| 1 |
| 3 |
∴AC=3DF,
∴-a=-3c,即c=
| 1 |
| 3 |
∵点A、D在反比例函数y=
| k |
| x |
∴k=ab=cd,∴d=3b.
∵d-b=
| 3 |
∴2b=
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
∴b=-
| ||
| 3 |
在Rt△ACB中,
∵∠BAC=60°,∴BC=AC•tan∠BAC=-
| 3 |
∵B点坐标为(0,4
| 3 |
| 3 |
∴OB=BC+OC=-
| 3 |
| 3 |
| ||
| 3 |
4
| ||
| 3 |
| 3 |
∴a=-3.
∴b=-
| ||
| 3 |
| 3 |
∴k=ab=-3×
| 3 |
| 3 |
故选:B.
点评:本题主要考查了反比例函数图象上点的坐标特征、锐角三角函数、相似三角形的判定与性质等知识,设点A的坐标为(a,b),根据条件得到b与a的等量关系是解决本题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 如图,两个同心圆的半径分别是5和3,∠AOB=140°,求阴影部分的面积.
如图,两个同心圆的半径分别是5和3,∠AOB=140°,求阴影部分的面积. 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=3,DC=4,BC=6,点E在射线BA上,若△EBC是以EB为腰的等腰三角形,则∠ECB的正切值
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=3,DC=4,BC=6,点E在射线BA上,若△EBC是以EB为腰的等腰三角形,则∠ECB的正切值 在平面直角坐标系中,二次函数y=ax2+bx+c的图象如图所示,对下列判断中正确的是
在平面直角坐标系中,二次函数y=ax2+bx+c的图象如图所示,对下列判断中正确的是 如图,在△ABC中,∠C=90°,∠A=60°,BC=15,解这个直角三角形.
如图,在△ABC中,∠C=90°,∠A=60°,BC=15,解这个直角三角形.