题目内容
已知△ABC的三边长分别为a、b、c，且a、b、c满足等式3（a2+b2+c2）=（a+b+c）2，试说明该三角形是等边三角形．
考点：因式分解的应用
专题：
分析：将已知等式左边去括号化简，右边利用完全平方公式展开，整理后再利用完全平方公式变形，根据非负数的性质，得到a=b=c，即可得到三角形为等边三角形．
解答：解：3（a2+b2+c2）=（a+b+c）2变形得：
3a2+3b2+3c2=a2+b2+c2+2ab+2ac+2bc，
3a2+3b2+3c2-a2-b2-c2-2ab-2ac-2bc=0，
整理得：（a-b）2+（a-c）2+（b-c）2=0，
∴a=b=c，
则△ABC为等边三角形．
3a2+3b2+3c2=a2+b2+c2+2ab+2ac+2bc，
3a2+3b2+3c2-a2-b2-c2-2ab-2ac-2bc=0，
整理得：（a-b）2+（a-c）2+（b-c）2=0，
∴a=b=c，
则△ABC为等边三角形．
点评：此题考查了因式分解的应用，非负数的性质，以及配方法的应用，完全平方公式的运用，熟练掌握公式及法则是解本题的关键．
练习册系列答案
相关题目
下列各数中-2，
，
，
，0.33，-
，0.1011011101…无理数的个数为（ ）
| π |
| 3 |
| 2 |
| 25 |
| 3 | 9 |
| A、4 | B、3 | C、1 | D、2 |
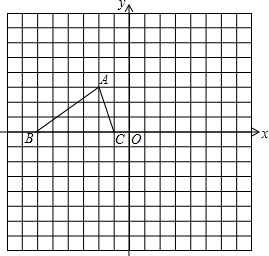如图所示，已知△ABC的三个顶点的坐标分别为A（-2，3），B（-6，0），C（-1，0）．
已知二次函数y=x2-（m-2）x+m的图象过点（-1，15），
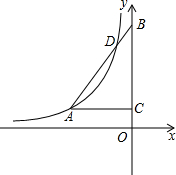如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，B、C均在y轴上，且B点坐标为（0，4
一块直角三角尺的形状与尺寸，若圆孔的半径为