题目内容
把两条长度相等的铁丝分别折成一个等边三角形和一个正方形,那么这个等边三角形和这个正方形的面积比为 .
考点:正方形的性质,等边三角形的性质
专题:
分析:设铁丝的长度为a,表示出等边三角形的边长和正方形的边长,然后根据等边三角形的性质和正方形的面积公式分别表示出两个图形的面积,再求出比值即可.
解答:解:设铁丝的长度为a,
则等边三角形的边长为
,高为
×
=
a,
等边三角形的面积=
•
•
a=
a2,
正方形的边长为
a,
面积=
a2,
所以,这个等边三角形和这个正方形的面积比为
a2:
a2=4
:9.
故答案为:4
:9.
则等边三角形的边长为
| a |
| 3 |
| ||
| 2 |
| a |
| 3 |
| ||
| 6 |
等边三角形的面积=
| 1 |
| 2 |
| a |
| 3 |
| ||
| 6 |
| ||
| 36 |
正方形的边长为
| 1 |
| 4 |
面积=
| 1 |
| 16 |
所以,这个等边三角形和这个正方形的面积比为
| ||
| 36 |
| 1 |
| 16 |
| 3 |
故答案为:4
| 3 |
点评:本题考查了正方形的性质,等边三角形的性质,熟记性质并用周长表示出面积是解题的关键.

练习册系列答案
相关题目
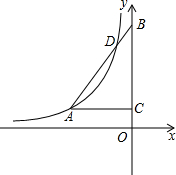 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,B、C均在y轴上,且B点坐标为(0,4
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,B、C均在y轴上,且B点坐标为(0,4| 3 |
| k |
| x |
| A、-3 | ||
B、-3
| ||
C、-2
| ||
D、-4
|
已知正整数a,其倒数
,相反数-a的大小关系正确的是( )
| 1 |
| a |
A、-a<
| ||
B、-a<
| ||
C、
| ||
D、-a≤a≤
|
下列说法错误的是( )
| A、2x2-3x-1是一个单项式 |
| B、2x2-3x-1是一个多项式 |
| C、2x2-3x-1是一个代数式 |
| D、2x2-3x-1是一个整式 |
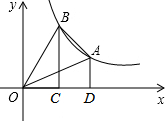 在反比例函数y=
在反比例函数y= 如图.AB是半圆O的直径,O为AB中点,C、D两点在弧AB上,且AD∥OC,连接BC、BD.若CD的度数为63°,求AD的度数.
如图.AB是半圆O的直径,O为AB中点,C、D两点在弧AB上,且AD∥OC,连接BC、BD.若CD的度数为63°,求AD的度数.