题目内容
1.按要求完成老师布置的两道作业题(1)计算:($\frac{1}{x}-\frac{{x}^{2}+2x+1}{{x}^{2}-1}$)÷$\frac{1}{x-1}$;
(2)解方程:$\frac{1}{x-2}+\frac{x-3}{2-x}=3$.
分析 (1)首先化简分式进而去括号求出即可;
(2)直接去分母,进而解方程即可,注意要检验.
解答 解:(1)($\frac{1}{x}-\frac{{x}^{2}+2x+1}{{x}^{2}-1}$)÷$\frac{1}{x-1}$
=[$\frac{1}{x}$-$\frac{(x+1)^{2}}{(x+1)(x-1)}$]×(x-1)
=($\frac{1}{x}$-$\frac{x+1}{x-1}$)×(x-1)
=$\frac{x-1}{x}$-x-1
=$\frac{-{x}^{2}-1}{x}$;
(2)$\frac{1}{x-2}+\frac{x-3}{2-x}=3$
去分母得:1-x+3=3(x-2),
解得:x=2.5,
检验:x=2.5时,x-2≠0,
即x=2.5是原方程的解.
点评 此题主要考查了分式的混合运算以及分式方程的解法,正确去分母是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列不属于分式$\frac{1}{2{x}^{2}-18}$与$\frac{x}{4x+12}$的公分母的是( )
| A. | (2x2-18)(4x+12) | B. | 16(x-3)(x+3) | C. | 4(x-3)(x+3) | D. | 2(x+3)(x-3) |
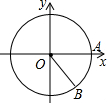 如图,以原点为圆心,2为半径的⊙O与正半轴交于点A,在⊙O上且在x轴的下方有一点B,∠AOB=45°,则点B的坐标为($\sqrt{2}$,$-\sqrt{2}$).
如图,以原点为圆心,2为半径的⊙O与正半轴交于点A,在⊙O上且在x轴的下方有一点B,∠AOB=45°,则点B的坐标为($\sqrt{2}$,$-\sqrt{2}$).