题目内容
7.在同一直线坐标系中,若正比例函数y=k1x的图象与反比例函数y=$\frac{{k}^{2}}{x}$的图象没有公共点,则( )| A. | k1+k2<0 | B. | k1+k2>0 | C. | k1k2<0 | D. | k1k2>0 |
分析 根据反比例函数与一次函数的交点问题,由于正比例函数y=k1x的图象与反比例函数y=$\frac{{k}^{2}}{x}$的图象没有公共点,则方程k1x=$\frac{{k}_{2}}{x}$没有实数解,把方程变形得到x2=$\frac{{k}_{2}}{{k}_{1}}$,于是得到k1与k2异号.
解答 解:根据题意,方程k1x=$\frac{{k}_{2}}{x}$没有实数解,
而x2=$\frac{{k}_{2}}{{k}_{1}}$,
所以k1与k2异号,即k1k2<0.
故选C.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
15.已知等腰三角形的两边长分别为5cm、3cm,则该等腰三角形的周长是( )
| A. | 13cm | B. | 11cm | C. | 13cm或者11cm | D. | 8cm |
2.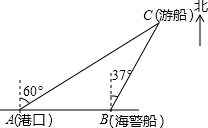 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )| A. | $\frac{1}{sin37°}$ | B. | $\frac{1}{cos37°}$ | C. | sin37° | D. | cos37° |
12.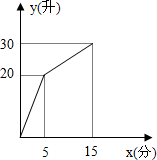 某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )
某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )
 某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )
某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )| A. | 22 | B. | 25 | C. | 27 | D. | 28 |
19.某中学毕业班准备给班级购买纪念礼物,现需从A、B两种礼物中挑选,A、B两种礼物的信息如下表所示:
(1)A、B两种礼物的单价分别为多少?
(2)只从实惠的角度来挑选的话,该挑选哪种礼物?说明理由.
| 礼物 | 数量(个) | 总价(元) |
| A | ab | a3b |
| B | 3a | 6a2b-3ab2 |
(2)只从实惠的角度来挑选的话,该挑选哪种礼物?说明理由.
17.不等式2x-7<5-2x的正整数解有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
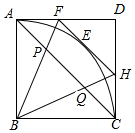 如图,正方形ABCD的边长为$\sqrt{2}$,点E是弧AC上的一个动点,过点E的切线与AD交于点F,与CD交于点H.
如图,正方形ABCD的边长为$\sqrt{2}$,点E是弧AC上的一个动点,过点E的切线与AD交于点F,与CD交于点H.  如图,AB是⊙O的直径,弦CD垂直平分半径OA,则∠ABC的大小为30度.
如图,AB是⊙O的直径,弦CD垂直平分半径OA,则∠ABC的大小为30度. 把下面四个图形拼成一个大长方形,并据此写出一个多项式的因式分解x2+3x+2=(x+2)(x+1).
把下面四个图形拼成一个大长方形,并据此写出一个多项式的因式分解x2+3x+2=(x+2)(x+1).