题目内容
12.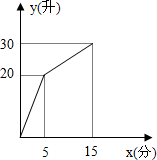 某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )
某数学课外活动小组利用一个有进水管与出水管的容器模拟水池蓄水情况:从某时刻开始,5分钟内只进水不出水,在随后的10分钟内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的蓄水量y(单位:L)与时间x(单位:min)之间的关系如图所示,则第12分钟容器内的蓄水量为( )| A. | 22 | B. | 25 | C. | 27 | D. | 28 |
分析 用待定系数法求出5≤x≤15对应的函数关系式,当x=12时,求出对应的值,即可解答.
解答 解:当5≤x≤15时,设y=kx+b,
把(5,20),(15,30)代入得:
$\left\{\begin{array}{l}{5k+b=20}\\{15k+b=30}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=1}\\{b=15}\end{array}\right.$
∴y=x+15,
当x=12时,y=12+15=27,
故选:C.
点评 本题考查了一次函数的应用,解决本题的关键是用待定系数法求出函数解析式.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
19.已知方程x2-5x-1=0的两根分别为x1与x2,则2x12-x1x2+2x22=( )
| A. | -10 | B. | -11 | C. | 55 | D. | 10 |
7.在同一直线坐标系中,若正比例函数y=k1x的图象与反比例函数y=$\frac{{k}^{2}}{x}$的图象没有公共点,则( )
| A. | k1+k2<0 | B. | k1+k2>0 | C. | k1k2<0 | D. | k1k2>0 |
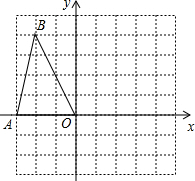 如图,正方形网格中的每一个小正方形的边长都是1,△AOB的三个顶点都在格点上,以O为坐标原点,建立如图平面直角坐标系,若把△AOB绕着点O顺时针旋转90°,得到△A1OB1,则点B旋转后的对应点B1的坐标为(4,2).
如图,正方形网格中的每一个小正方形的边长都是1,△AOB的三个顶点都在格点上,以O为坐标原点,建立如图平面直角坐标系,若把△AOB绕着点O顺时针旋转90°,得到△A1OB1,则点B旋转后的对应点B1的坐标为(4,2).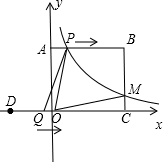 如图,平面直角坐标系(单位:cm)中,B(5,4),D(-3,0),过B作BC⊥x轴于C,BA⊥y轴于A,点P从点A出发,以每秒1cm的速度沿A→B方向向终点B运动;点Q从点D出发,以每秒2cm的速度沿D→C方向向终点C运动,已知动点P、Q同时出发,当点P,点Q有一点到达终点时,P、Q都停止运动,设运动时间为t秒.
如图,平面直角坐标系(单位:cm)中,B(5,4),D(-3,0),过B作BC⊥x轴于C,BA⊥y轴于A,点P从点A出发,以每秒1cm的速度沿A→B方向向终点B运动;点Q从点D出发,以每秒2cm的速度沿D→C方向向终点C运动,已知动点P、Q同时出发,当点P,点Q有一点到达终点时,P、Q都停止运动,设运动时间为t秒. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长(小于AB的长)为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长(小于AB的长)为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.