题目内容
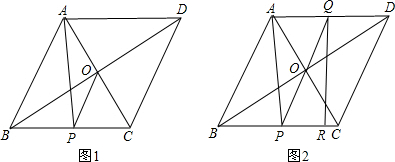
15. 如图,AB是⊙O的直径,弦CD垂直平分半径OA,则∠ABC的大小为30度.
如图,AB是⊙O的直径,弦CD垂直平分半径OA,则∠ABC的大小为30度.
分析 根据线段的特殊关系求角的大小,再运用圆周角定理求解.
解答  解:连接OC,∵弦CD垂直平分半径OA,
解:连接OC,∵弦CD垂直平分半径OA,
∴OE=$\frac{1}{2}$OC,
∴∠OCD=30°,∠AOC=60°,
∴∠ABC=30°.
故答案为:30.
点评 本题主要是利用直角三角形中特殊角的三角函数先求出∠OCE=30°,∠EOC=60°.然后再圆周角定理,从而求出∠ABC=30°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.使二次根式$\sqrt{x-1}$的有意义的x的取值范围是( )
| A. | x>0 | B. | x>1 | C. | x≥1 | D. | x≠1 |
7.在同一直线坐标系中,若正比例函数y=k1x的图象与反比例函数y=$\frac{{k}^{2}}{x}$的图象没有公共点,则( )
| A. | k1+k2<0 | B. | k1+k2>0 | C. | k1k2<0 | D. | k1k2>0 |
8. 如图,点A、点B、点C均在⊙O上,若∠B=40°,则∠AOC的度数为( )
如图,点A、点B、点C均在⊙O上,若∠B=40°,则∠AOC的度数为( )
 如图,点A、点B、点C均在⊙O上,若∠B=40°,则∠AOC的度数为( )
如图,点A、点B、点C均在⊙O上,若∠B=40°,则∠AOC的度数为( )| A. | 40° | B. | 60° | C. | 80° | D. | 90° |
 已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y
已知如图,在矩形ABCD中,P是边AD上的一动点,连结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD与点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x(2<x≤5),PM=y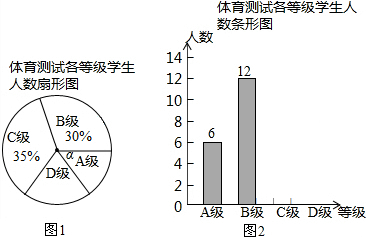
 (1)计算:$\sqrt{8}$-(π-1)0-4sin45°;
(1)计算:$\sqrt{8}$-(π-1)0-4sin45°;