题目内容
2.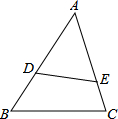 若△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC=15.
若△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC=15.
分析 根据△ADE∽△ACB,得到$\frac{AD}{AC}$=$\frac{DE}{BC}$,代入已知数据计算即可.
解答 解:∵△ADE∽△ACB,
∴$\frac{AD}{AC}$=$\frac{DE}{BC}$,又$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,
∴BC=15.
故答案为:15.
点评 本题考查的是相似三角形的性质,掌握相似三角形的对应边的比相等并找准对应边是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
13.标号为A、B、C、D的四个盒子中所装有白球和黑球数如下,则下列盒子最易摸到黑球的是( )
| A. | 9个黑球和3个白球 | B. | 10黑球和10个白球 | ||
| C. | 12个黑球和6个白球 | D. | 10个黑球和5个白球 |
10. 在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
 在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
14.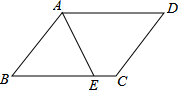 如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
 如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 4cm |
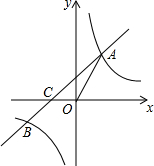 如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A和点B(-2,n),与x轴交于点C(-1,0),连接OA.
如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A和点B(-2,n),与x轴交于点C(-1,0),连接OA.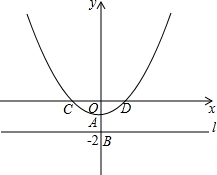 如图,在平面直角坐标系xOy中,直线l⊥y轴于点B(0,-2),A为OB的中点,以A为顶点的抛物线y=ax2+c与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
如图,在平面直角坐标系xOy中,直线l⊥y轴于点B(0,-2),A为OB的中点,以A为顶点的抛物线y=ax2+c与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.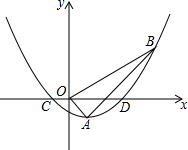 如图,在平面直角坐标系中,顶点为A(1,-1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).
如图,在平面直角坐标系中,顶点为A(1,-1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).