题目内容
7.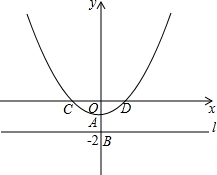 如图,在平面直角坐标系xOy中,直线l⊥y轴于点B(0,-2),A为OB的中点,以A为顶点的抛物线y=ax2+c与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
如图,在平面直角坐标系xOy中,直线l⊥y轴于点B(0,-2),A为OB的中点,以A为顶点的抛物线y=ax2+c与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.(1)求抛物线的解析式;
(2)若⊙P与y轴的另一交点为E,且OE=2,求点P的坐标;
(3)判断直线l与⊙P的位置关系,并说明理由.
分析 (1)根据题意可知A(0,-1),C(-2,0),D(2,0),从而可求得抛物线的解析式;
(2)根据OE=2可知点E的坐标为(0,2)或(0,-2),从而可确定出点P的纵坐标为1或-1;
(3)设点P的坐标为(m,$\frac{1}{4}{m}^{2}-1$),然后求得圆P的半径OP和点P到直线l的距离,根据d=r,可知直线和圆相切.
解答 解:(1)∵点A为OB的中点,
∴点A的坐标为(0,-1).
∵CD=4,由抛物线的对称性可知:点C(-2,0),D(2,0),
将点A(0,-1),C(-2,0),D(2,0)代入抛物线的解析式得:$\left\{\begin{array}{l}{c=-1}\\{4a+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{c=-1}\\{a=\frac{1}{4}}\end{array}\right.$,
∴抛物线得解析式为y=$\frac{1}{4}{x}^{2}-1$.
(2)如下图:过点P1作P1F⊥OE.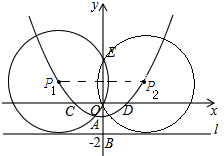
∵OE=2,
∴点E的坐标为(0,2).
∵P1F⊥OE.
∴EF=OF.
∴点P1的纵坐标为1.
同理点P2的纵坐标为1.
将y=1代入抛物线的解析式得:x1=$-2\sqrt{2}$,x2=2$\sqrt{2}$.
∴点P1(-2$\sqrt{2}$,1),P2(2$\sqrt{2}$,1).
如下图: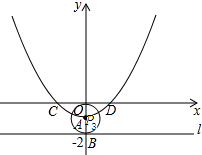
当点E与点B重合时,点P3与点A重合,
∴点P3的坐标为(0,-1).
综上所述点P的坐标为(-2$\sqrt{2}$,1)或(2$\sqrt{2}$,1)或(0,-1).
(3)设点P的坐标为(m,$\frac{1}{4}{m}^{2}-1$),
∴圆的半径OP=$\sqrt{{m}^{2}+(\frac{1}{4}{m}^{2}-1)^{2}}$=$\frac{{m}^{2}}{4}+1$,
点P到直线l的距离=$\frac{1}{4}{m}^{2}-1$-(-2)=$\frac{{m}^{2}}{4}$+1.
∴d=r.
∴直线l与圆P相切.
点评 本题主要考查的是二次函数与圆的综合应用,根据题意确定出点E的坐标,然后再得出点P的纵坐标是解题的关键.

| A. | 3m+2n=5mn | B. | (ab2)3=a3b5 | C. | x5•x=x6 | D. | y3÷y3=y |

| A. | 147.40元 | B. | 143.17元 | C. | 144.23元 | D. | 136.83元 |
| A. | y=$\frac{1}{x}$ | B. | y=-2x-3 | C. | y=2x2+1 | D. | y=5x |
 如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为15π.
如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为15π.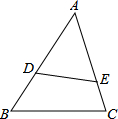 若△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC=15.
若△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC=15.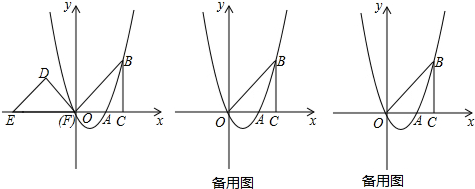
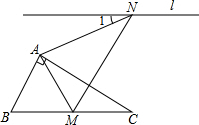 如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,过点N的直线l∥BC,则∠1的度数为( )
如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,过点N的直线l∥BC,则∠1的度数为( )