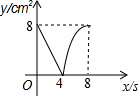题目内容
17.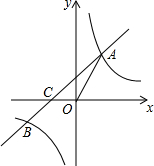 如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A和点B(-2,n),与x轴交于点C(-1,0),连接OA.
如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A和点B(-2,n),与x轴交于点C(-1,0),连接OA.(1)求一次函数和反比例函数的解析式;
(2)若点P在坐标轴上,且满足PA=OA,求点P的坐标.
分析 (1)把C(-1,0)代入y=x+b,求出b的值,得到一次函数的解析式;再求出B点坐标,然后将B点坐标代入y=$\frac{k}{x}$,利用待定系数法即可求出反比例函数的解析式;
(2)先将反比例函数与一次函数的解析式联立,求出A点坐标,再分①点P在x轴上;②点P在y轴上;两种情况进行讨论.
解答 解:(1)∵一次函数y=x+b的图象与x轴交于点C(-1,0),
∴-1+b=0,解得b=1,
∴一次函数的解析式为y=x+1,
∵一次函数y=x+1的图象过点B(-2,n),
∴n=-2+1=-1,
∴B(-2,-1).
∵反比例函数y=$\frac{k}{x}$的图象过点B(-2,-1),
∴k=-2×(-1)=2,
∴反比例函数的解析式为y=$\frac{2}{x}$;
(2)由$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{2}{x}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,或$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$,
∵B(-2,-1),
∴A(1,2).
分两种情况:
①如果点P在x轴上,设点P的坐标为(x,0),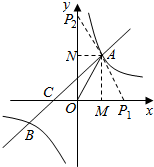
∵P1A=OA,
∴P1O=2OM,
∴点P1的坐标为(2,0);
②如果点P在y轴上,设点P的坐标为(0,y),
∵P2A=OA,
∴P2O=2NO,
∴点P的坐标为(0,4);
综上所述,所求点P的坐标为(2,0)或(0,4).
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.利用待定系数法正确求出反比例函数与一次函数的解析式是解题的关键.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案| A. | π | B. | 2π | C. | 4π | D. | 6π |
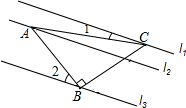 如图所示,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点分别在相互平行的三条直线l1、l2、l3上,且∠1=15°,则∠2=30度.
如图所示,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点分别在相互平行的三条直线l1、l2、l3上,且∠1=15°,则∠2=30度. 如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB=$\frac{7}{13}$.
如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB=$\frac{7}{13}$.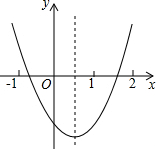 如图,观察二次函数y=ax2+bx+c的图象,下列结论:
如图,观察二次函数y=ax2+bx+c的图象,下列结论: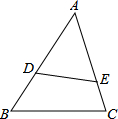 若△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC=15.
若△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC=15.
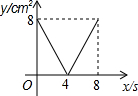
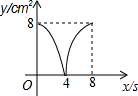
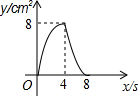
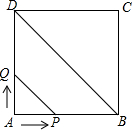 如图,正方形ABCD的边长为4cm,动点p,Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为( )
如图,正方形ABCD的边长为4cm,动点p,Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为( )