题目内容
10. 在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )
在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是( )| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
分析 由条件可以知道DE是△ABC的中位线,根据中位线的性质就可以求出$\frac{DE}{BC}=\frac{1}{2}$,再根据相似三角形的性质就可以得出结论.
解答 解:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,$\frac{DE}{BC}=\frac{1}{2}$,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}=(\frac{1}{2})^{2}$,
∵△ADE的面积为4,
∴$\frac{4}{{S}_{△ABC}}=\frac{1}{4}$,
∴S△ABC=16.
故选:C.
点评 本题考查中位线的判定及性质的运用,相似三角形的判定及性质的运用,解答时证明△ADE∽△ABC是解答本题的关键.

练习册系列答案
相关题目
18.如图,这是某用户银行存折中2012年11月到2013年5月间代扣电费的相关数据,从中可以看出扣缴电费最多的一次达到( )


| A. | 147.40元 | B. | 143.17元 | C. | 144.23元 | D. | 136.83元 |
1.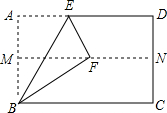 如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )
如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )
 如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )
如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 36° |
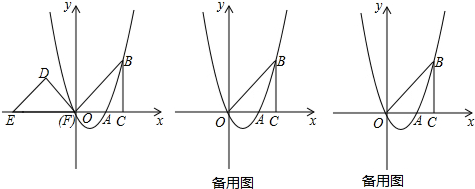
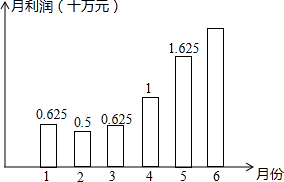 甲、乙两玩具厂从已有订单来看,两厂都预计自2011年起本厂的月利润y(十万元)与月份x之间满足一定的函数关系.甲厂预测的关系:y=$\frac{1}{8}$x2-x+2;乙厂则预测该厂的月利润与月份也满足二次函数关系,且图象形状与甲厂的相同.又知乙厂预测的该厂前几个月份的月利润如图所示,试根据上述信息解决下列问题:
甲、乙两玩具厂从已有订单来看,两厂都预计自2011年起本厂的月利润y(十万元)与月份x之间满足一定的函数关系.甲厂预测的关系:y=$\frac{1}{8}$x2-x+2;乙厂则预测该厂的月利润与月份也满足二次函数关系,且图象形状与甲厂的相同.又知乙厂预测的该厂前几个月份的月利润如图所示,试根据上述信息解决下列问题: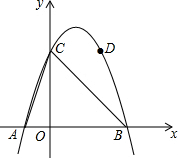 某拱桥横截面为抛物线形,将抛物线放置在平面直角坐标系中如图所示,抛物线与x轴交于A、B两点,与y轴交于C点,且抛物线的解析式为y=-x2+2x+3.
某拱桥横截面为抛物线形,将抛物线放置在平面直角坐标系中如图所示,抛物线与x轴交于A、B两点,与y轴交于C点,且抛物线的解析式为y=-x2+2x+3. 如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB=$\frac{7}{13}$.
如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB=$\frac{7}{13}$. 如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为15π.
如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为15π.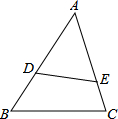 若△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC=15.
若△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC=15.