题目内容
14.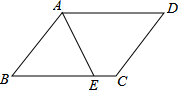 如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 4cm |
分析 根据平行四边形的性质得出AB=CD,AD=BC,AD∥BC,推出∠DAE=∠BAE,求出∠BAE=∠AEB,推出AB=BE,设AB=CD=xcm,则AD=BC=(x+2)cm,得出方程x+x+2=10,求出方程的解即可.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∴∠DAE=∠BAE,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=BE,
设AB=CD=xcm,则AD=BC=(x+2)cm,
∵?ABCD的周长为20cm,
∴x+x+2=10,
解得:x=4,
即AB=4cm,
故选D.
点评 本题考查了平行四边形的在,平行线的性质,等腰三角形的判定的应用,解此题的关键是能推出AB=BE,题目比较好,难度适中.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
6.在半径为6的⊙O中,60°圆心角所对的弧长是( )
| A. | π | B. | 2π | C. | 4π | D. | 6π |
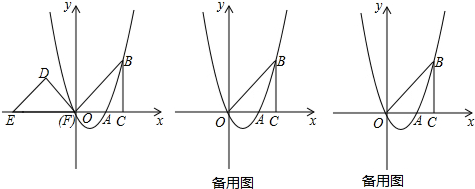
 已知一次函数y=-2x+a与y=x+b的图象如图所示,则关于x的不等式-2x+a≤x+b的解集是x≥-1.
已知一次函数y=-2x+a与y=x+b的图象如图所示,则关于x的不等式-2x+a≤x+b的解集是x≥-1. 如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB=$\frac{7}{13}$.
如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB=$\frac{7}{13}$.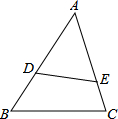 若△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC=15.
若△ADE∽△ACB,且$\frac{AD}{AC}$=$\frac{2}{3}$,DE=10,则BC=15.
 如图所示,将正五边形ABCDE绕点C按顺时针方向最少旋转72度后顶点D会落在直线BC上.
如图所示,将正五边形ABCDE绕点C按顺时针方向最少旋转72度后顶点D会落在直线BC上.