题目内容
15.已知a+b=-c,则a($\frac{1}{b}$+$\frac{1}{c}$)+b($\frac{1}{a}$+$\frac{1}{c}$)+c($\frac{1}{a}$+$\frac{1}{b}$)的值是多少?分析 原式整理后,利用同分母分式的加法法则计算,将已知等式变形后代入计算即可求出值.
解答 解:由a+b=-c,得到b+c=-a,a+c=-b,
则原式=$\frac{a}{b}$+$\frac{a}{c}$+$\frac{b}{a}$+$\frac{b}{c}$+$\frac{c}{a}$+$\frac{c}{b}$
=$\frac{b+c}{a}$+$\frac{a+c}{b}$+$\frac{a+b}{c}$
=-1-1-1
=-3.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.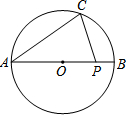 如图,AB是⊙O的直径,点C在圆周上,点P是线段OB上任意一点,连结AC、CP.若∠BAC=35°,则∠APC的度数不可能是( )
如图,AB是⊙O的直径,点C在圆周上,点P是线段OB上任意一点,连结AC、CP.若∠BAC=35°,则∠APC的度数不可能是( )
 如图,AB是⊙O的直径,点C在圆周上,点P是线段OB上任意一点,连结AC、CP.若∠BAC=35°,则∠APC的度数不可能是( )
如图,AB是⊙O的直径,点C在圆周上,点P是线段OB上任意一点,连结AC、CP.若∠BAC=35°,则∠APC的度数不可能是( )| A. | 90° | B. | 75° | C. | 60° | D. | 50° |
17.等式(a+1)0=1的条件是( )
| A. | a≠-1 | B. | a≠0 | C. | a≠1 | D. | a=-1 |
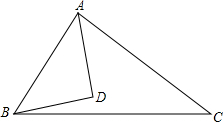 如图,在△ABC中,AD是∠A的平分线,BD⊥AD,AB=12,AC=18
如图,在△ABC中,AD是∠A的平分线,BD⊥AD,AB=12,AC=18