题目内容
8.(1)已知x=$\sqrt{5}$+2,求代数式(9-4$\sqrt{5}$)x2+(2-$\sqrt{5}$)x+$\sqrt{5}$的值.(2)先化简,再求值:(a2b+ab)÷$\frac{{a}^{2}+2a+1}{a+1}$,其中a=$\sqrt{5}$+2,b=$\sqrt{5}$-2.
分析 (1)直接代入,利用完全平方公式以及平方差公式计算即可.
(2)先化简,然后代入计算即可.
解答 解:(1)原式=(9-4$\sqrt{5}$)($\sqrt{5}$+2)2+(2-$\sqrt{5}$)(2+$\sqrt{5}$)+$\sqrt{5}$
=(9-4$\sqrt{5}$)(9+4$\sqrt{5}$)+22-($\sqrt{5}$)2+$\sqrt{5}$
=92-(4$\sqrt{5}$)2+4-5+$\sqrt{5}$
=81-80-1+$\sqrt{5}$
=$\sqrt{5}$
(2)原式=ab(a+1)÷$\frac{(a+1)^{2}}{a+1}$
=ab(a+1)÷(a+1)
=ab,
∵a=$\sqrt{5}$+2,b=$\sqrt{5}$-2,
∴上式=($\sqrt{5}$+2)($\sqrt{5}$-2)=5-4=1.
点评 本题考查二次根式的化简求值、乘法公式等知识,解题的关键是熟练应用乘法公式,掌握二次根式的混合运算法则,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列图形中,∠1和∠2是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在?ABCD中,AE⊥BC,AF⊥CD,E,F为垂足,若∠EAF=59°,则∠B=59度.
如图,在?ABCD中,AE⊥BC,AF⊥CD,E,F为垂足,若∠EAF=59°,则∠B=59度.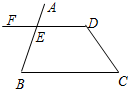 如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.
如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.