题目内容
18.在已知线段AB的同侧构造∠FAB=∠GBA,并且在射线AF,BG上分别取点D和E,在线段AB上取点C,连结DC和EC.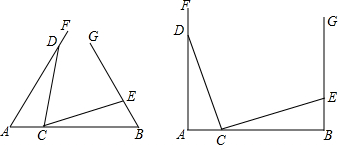
(1)如图,若AD=3,BE=1,△ADC≌△BCE.在∠FAB=∠GBA=60°或∠FAB=∠GBA=90°两种情况中任选一种,解决以下问题:
①线段AB的长度是否发生变化,直接写出长度或变化范围;
②∠DCE的度数是否发生变化,直接写出度数或变化范围.
(2)若AD=a,BE=b,∠FAB=∠GBA=α,且△ADC和△BCE这两个三角形全等,请求出:
①线段AB的长度或取值范围,并说明理由;
②∠DCE的度数或取值范围,并说明理由.
分析 (1)选第一个图:①由全等三角形的性质得出AC=BE=1,BC=AD=3,得出AB=AC+BC=4;
②由全等三角形的性质得出∠ADC=∠BCE,由三角形的外角性质得出∠BCD=∠A+∠ADC=∠DCE+∠BCE,得出∠DCE=∠A=60°即可;
若选第二个图时,方法同第一个图的解法;
(2)当a≠b时,①由全等三角形的性质得出AC=BE=b,BC=AD=a,得出AB=AC+BC=a+b即可;
②由全等三角形的性质得出∠ADC=∠BCE,由三角形的外角性质得出∠BCD=∠A+∠ADC=∠DCE+∠BCE,得出∠DCE=∠A=α即可;
当a=b时,①AB>0,由全等三角形的性质得出AC=BE=b,BC=AD=a,得出AB=AC+BC=a+b>0即可;
②由全等三角形的性质得出∠ADC=∠BCE,由三角形的外角性质得出∠BCD=∠A+∠ADC=∠DCE+∠BCE,得出∠DCE=∠A=α,即可得出0°<∠DCE<180°.
解答 解:(1)选第一个图:
①线段AB的长度不发生变化,AB=4;理由如下:
∵AD=3,BE=1,△ADC≌△BCE.
∴AC=BE=1,BC=AD=3,
∴AB=AC+BC=4;
②∠DCE的度数不发生变化,∠DCE=60°;理由如下:
∵△ADC≌△BCE,
∴∠ADC=∠BCE,
∵∠BCD=∠A+∠ADC=∠DCE+∠BCE,
∴∠DCE=∠A=60°;
若选第二个图:
①线段AB的长度不发生变化,AB=4;理由如下:
∵AD=3,BE=1,△ADC≌△BCE.
∴AC=BE=1,BC=AD=3,
∴AB=AC+BC=4;
②∠DCE的度数不发生变化,∠DCE=90°;理由如下:
∵△ADC≌△BCE,
∴∠ADC=∠BCE,
∵∠BCD=∠A+∠ADC=∠DCE+∠BCE,
∴∠DCE=∠A=90°;
(2)当a≠b时,①AB=a+b,理由如下:
∵AD=a,BE=b,△ADC≌△BCE.
∴AC=BE=b,BC=AD=a,
∴AB=AC+BC=a+b;
②∠DCE=α,理由如下:
∵△ADC≌△BCE,
∴∠ADC=∠BCE,
∵∠BCD=∠A+∠ADC=∠DCE+∠BCE,
∴∠DCE=∠A=α;
当a=b时,①AB>0,理由如下:
∵AD=a,BE=b,△ADC≌△BCE.
∴AC=BE=b,BC=AD=a,
∴AB=AC+BC=a+b>0;
②0°<∠DCE<180°.理由如下:
∵△ADC≌△BCE,
∴∠ADC=∠BCE,
∵∠BCD=∠A+∠ADC=∠DCE+∠BCE,
∴∠DCE=∠A=α,
∵0°<α<180°.
∴0°<∠DCE<180°.
点评 本题是三角形综合题目,考查了全等三角形的性质、三角形的外角性质等知识;熟练掌握全等三角形的性质和三角形的外角性质是解决问题的关键.

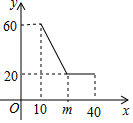 经市场调查,某公司生产的大白公仔的每天的销售量y(件)与销售价格x(元/件)之间的函数关系如图所示.
经市场调查,某公司生产的大白公仔的每天的销售量y(件)与销售价格x(元/件)之间的函数关系如图所示.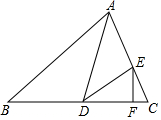 如图,在△ABC中,∠B=50°,AD平分∠CAB,交BC于D,E为AC边上一点,连接DE,∠EAD=∠EDA,EF⊥BC于点F.求∠FED的度数.
如图,在△ABC中,∠B=50°,AD平分∠CAB,交BC于D,E为AC边上一点,连接DE,∠EAD=∠EDA,EF⊥BC于点F.求∠FED的度数.
 如图,点D是CB延长线上一点,已知BE平分∠ABD,∠C=62°,∠ABD=124°,则BE∥AC吗?请说明理由.
如图,点D是CB延长线上一点,已知BE平分∠ABD,∠C=62°,∠ABD=124°,则BE∥AC吗?请说明理由.