题目内容
4.两数和的平方公式(a+b)2=a2+2ab+b2.(1)请你根据数形结合的思想,自己画图,利用图形的面积表示说明此公式.
(2)利用此公式求(a-b)2.
分析 (1)从整体看大正方形的面积为边长a+b的平方,从部分看大正方形的面积为边长为a和b的两个小正方形与长为a、宽为b的两个长方形的面积和,据此可得;
(2)将原式改写成[a+(-b)]2,再利用(1)中公式求解可得.
解答 解:(1)如图所示,
大正方形的面积为(a+b)2,或者a2+ab+ab+b2=a2+2ab+b2,
∴(a+b)2=a2+2ab+b2;
(2)(a-b)2=[a+(-b)]2
=a2+2•a•(-b)+(-b)2
=a2-2ab+b2.
点评 本题主要考查完全平方公式的几何背景,应从整体和部分两方面来理解完全平方公式的几何意义,主要围绕图形面积展开分析.

练习册系列答案
相关题目
15.如图中的轴对称图形有( )


| A. | (1)(2) | B. | (2),(3) | C. | (1),(4) | D. | (3),(4) |
9. 如图,在下列给出的条件中,不能判定AB∥DF的是( )
如图,在下列给出的条件中,不能判定AB∥DF的是( )
 如图,在下列给出的条件中,不能判定AB∥DF的是( )
如图,在下列给出的条件中,不能判定AB∥DF的是( )| A. | ∠1=∠A | B. | ∠A=∠3 | C. | ∠1=∠4 | D. | ∠A+∠2=180° |
16.用代数式表示“a与b两数的差的平方”,正确的是( )
| A. | a2-b | B. | a-b2 | C. | a2-b2 | D. | (a-b)2 |
13.已知在等腰三角形ABC中,AB=AC=10,一个底角的余切值为$\frac{3}{4}$,那么这个等腰三角形的底边长等于( )
| A. | 12 | B. | 16 | C. | $\frac{30}{17}\sqrt{34}$ | D. | $\frac{50}{17}\sqrt{34}$ |
14.在下列叙述中,正确的是( )
| A. | 任何有理数都有相反数 | |
| B. | 如果-15米表示向东前进了15米,那么10米表示向北前进了10米 | |
| C. | 离原点近的点所对应的有理数较小 | |
| D. | 有最大的负数,没有最小的正数 |
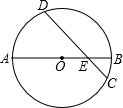 如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4$\sqrt{2}$,求
如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4$\sqrt{2}$,求 化简求值:
化简求值: