题目内容
19.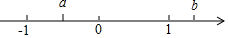 化简求值:
化简求值:(1)已知a是$\sqrt{13}$的整数部分,$\sqrt{b}$=3,求$\sqrt{ab+54}$的平方根.
(2)已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.
分析 (1)由于3<$\sqrt{13}$<4,由此可得$\sqrt{13}$的整数a的值;由于$\sqrt{b}$=3,根据算术平方根的定义可求b,再代入$\sqrt{ab+54}$计算,进一步求得平方根.
(2)利用数轴得出各项符号,进而利用二次根式和绝对值的性质化简求出即可.
解答 解:(1)∵3<$\sqrt{13}$<4,
∴a=3,
∵$\sqrt{b}$=3,
∴b=9,
∴$\sqrt{ab+54}$=$\sqrt{3×9+54}$=9,
∴$\sqrt{ab+54}$的平方根是±3;
(2)由数轴可得:-1<a<0<1<b,
则a+1<0,b-1>0,a-b<0,
则$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|
=-a-1+2(b-1)+(a-b)
=-a-1+2b-2+a-b
=b-3.
点评 本题考查了算术平方根与平方根的定义和估算无理数的大小,熟记概念,先判断所给的无理数的近似值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7. 如图,一座石拱桥是圆弧形其跨度AB=24米,半径为13米,则拱高CD为( )
如图,一座石拱桥是圆弧形其跨度AB=24米,半径为13米,则拱高CD为( )
 如图,一座石拱桥是圆弧形其跨度AB=24米,半径为13米,则拱高CD为( )
如图,一座石拱桥是圆弧形其跨度AB=24米,半径为13米,则拱高CD为( )| A. | 3$\sqrt{5}$米 | B. | 5米 | C. | 7米 | D. | 8米 |
 如图,沿长方形ABCD的对角线AC对折,点B落在点E上,AE与CD交于F点,
如图,沿长方形ABCD的对角线AC对折,点B落在点E上,AE与CD交于F点,



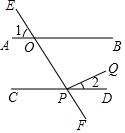 如图,直线AB、CD被直线EF所截,交点为O、P,PQ⊥EF,垂足为P,如果∠1=60°,∠2=30°,那么直线AB、CD平行吗?为什么?
如图,直线AB、CD被直线EF所截,交点为O、P,PQ⊥EF,垂足为P,如果∠1=60°,∠2=30°,那么直线AB、CD平行吗?为什么?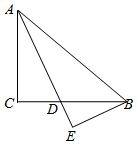 已知:如图,在△ABC中,∠C=90°,AE平分∠CAB,且BE2=DE•AE.求证:BE⊥AE.
已知:如图,在△ABC中,∠C=90°,AE平分∠CAB,且BE2=DE•AE.求证:BE⊥AE.