题目内容
13.已知在等腰三角形ABC中,AB=AC=10,一个底角的余切值为$\frac{3}{4}$,那么这个等腰三角形的底边长等于( )| A. | 12 | B. | 16 | C. | $\frac{30}{17}\sqrt{34}$ | D. | $\frac{50}{17}\sqrt{34}$ |
分析 根据题意可以画出相应的图形,从而可以求得底边的长,本题得以解决.
解答  解:如右图所示,
解:如右图所示,
∵在等腰三角形ABC中,AB=AC=10,一个底角的余切值为$\frac{3}{4}$,
设BD=3a,则AD=4a,
∴(3a)2+(4a)2=102,
解得,a=2,
∴3a=6,
即BD=6,
∴BC=2BD=12,
故选A.
点评 本题考查解直角三角形、等腰三角形的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
3.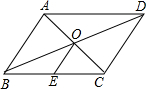 如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
 如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 3 cm | B. | 6 cm | C. | 9 cm | D. | 12 cm |
 如图,AB与CD相交于点O,∠EOB=35°,∠AOD=125°,求证CD⊥EO.
如图,AB与CD相交于点O,∠EOB=35°,∠AOD=125°,求证CD⊥EO.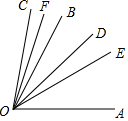 已知∠BOC在∠AOB的外部,OE平分∠AOB,OF平分∠BOC,OD平分∠AOC,∠AOE=30°,∠BOD=20°,试求∠COF的度数,下面是李小雨同学的解题过程:
已知∠BOC在∠AOB的外部,OE平分∠AOB,OF平分∠BOC,OD平分∠AOC,∠AOE=30°,∠BOD=20°,试求∠COF的度数,下面是李小雨同学的解题过程: