题目内容
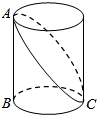 如图,已知圆柱底面的周长为4分米,圆柱高为2分米,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长度最短为
如图,已知圆柱底面的周长为4分米,圆柱高为2分米,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长度最短为考点:平面展开-最短路径问题
专题:
分析:要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.
解答: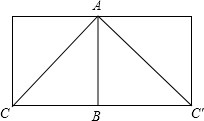 解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
∵圆柱底面的周长为4dm,圆柱高为2dm,
∴AB=2dm,BC=BC′=2dm,
∴AC2=22+22=4+4=8,
∴AC=2
dm,
∴这圈金属丝的周长最小为2AC=4
dm.
故答案为:4
.
 解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.∵圆柱底面的周长为4dm,圆柱高为2dm,
∴AB=2dm,BC=BC′=2dm,
∴AC2=22+22=4+4=8,
∴AC=2
| 2 |
∴这圈金属丝的周长最小为2AC=4
| 2 |
故答案为:4
| 2 |
点评:本题考查了平面展开-最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )| A、两点之间线段最短 |
| B、两点确定一条直线 |
| C、垂线段最短 |
| D、以上都不是 |
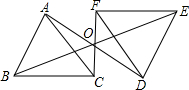 如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )
如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )| A、点A与点D是对应点 |
| B、BO=EO |
| C、∠ACB=∠FDE |
| D、AB∥DE |
 如图L1∥L2∥L3,AB=4,DE=3,EF=6,则BC的长( )
如图L1∥L2∥L3,AB=4,DE=3,EF=6,则BC的长( )| A、4 | B、6 | C、8 | D、10 |
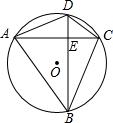 如图,四边形ABCD是⊙O的内接四边形,AC⊥BD于点E,若AB=8,CD=6,则⊙O的半径是多少?
如图,四边形ABCD是⊙O的内接四边形,AC⊥BD于点E,若AB=8,CD=6,则⊙O的半径是多少? 如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,AB于CD相交于点O,若∠A=40°,∠C=36°,求∠P的度数.
如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,AB于CD相交于点O,若∠A=40°,∠C=36°,求∠P的度数.