题目内容
10.化简:$\frac{1}{x(x+1)}$+$\frac{1}{(x+1)(x+2)}$+$\frac{1}{(x+2)(x+3)}$.分析 根据所化简的式子观察可以分开相减,观察规律,可以对所求式子化简,本题得以解决.
解答 解:$\frac{1}{x(x+1)}$+$\frac{1}{(x+1)(x+2)}$+$\frac{1}{(x+2)(x+3)}$
=$(\frac{1}{x}-\frac{1}{x+1})+(\frac{1}{x+1}-\frac{1}{x+2})+(\frac{1}{x+2}-\frac{1}{x+3})$
=$\frac{1}{x}-\frac{1}{x+1}+\frac{1}{x+1}-\frac{1}{x+2}+\frac{1}{x+2}-\frac{1}{x+3}$
=$\frac{1}{x}-\frac{1}{x+3}$
=$\frac{3}{x(x+3)}$
=$\frac{3}{{x}^{2}+3x}$.
点评 本题考查分式的加减法,解题的关键是明确分式加减法的计算方法.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
20.已知正△ABC内接于圆O,四边形DEFG为半圆O的内接正方形(D,E在直径上,F,G在半圆上的正方形),S△ABC=a,S四边形DEFG=b,则$\frac{a}{b}$的值等于( )
| A. | 2 | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3\sqrt{3}}{5}$ | D. | $\frac{15\sqrt{3}}{16}$ |
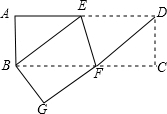 如图,将矩形纸片ABCD沿EF折叠,使D与B重合,折痕为EF,然后展开,连接DF,BE.
如图,将矩形纸片ABCD沿EF折叠,使D与B重合,折痕为EF,然后展开,连接DF,BE. 如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为7.
如图,在?ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD边上的点F.若△FDE的周长为8,△FCB的周长为22,则FC的长为7. 如图,已知一次函数y=kx+b的图象与x轴交于点A(5,0),与函数y=2x的图象交于点M,点M的横坐标为2,求点M的坐标及函数y=kx+b的表达式.
如图,已知一次函数y=kx+b的图象与x轴交于点A(5,0),与函数y=2x的图象交于点M,点M的横坐标为2,求点M的坐标及函数y=kx+b的表达式.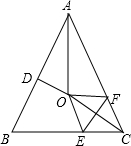 如图,在△ABC中,AB=AC,∠BAC=58°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠BEO的度数是64°.
如图,在△ABC中,AB=AC,∠BAC=58°,∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠BEO的度数是64°.