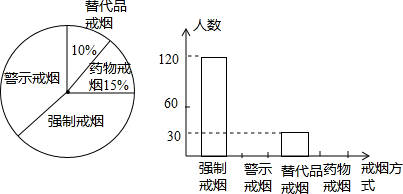
题目内容
10.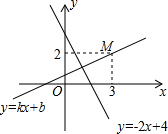 如图,一次函数y=kx+b(k≠0)的图象经过点M(3,2),且与一次函数y=-2x+4的图象交于点N.若对于一次函数y=kx+b(k≠0),当y随x的增大而增大时,则点N的横坐标的取值范围是1<x<3.
如图,一次函数y=kx+b(k≠0)的图象经过点M(3,2),且与一次函数y=-2x+4的图象交于点N.若对于一次函数y=kx+b(k≠0),当y随x的增大而增大时,则点N的横坐标的取值范围是1<x<3.
分析 把M点坐标代入可得到关于k、b的关系式,再联立两直线解析式,消去y可求得x,可得到关于k的函数,再结合k的范围可求得x的范围,可得出答案.
解答 解:
∵y=kx+b(k≠0)的图象经过点M(3,2),
∴2=3k+b,解得b=2-3k,
∴一次函数解析式为y=kx+2-3k,
联立两函数解析式可得$\left\{\begin{array}{l}{y=-2x+4}\\{y=kx+2-3k}\end{array}\right.$,消去y整理可得(k+2)x=3k+2,
∴x=$\frac{3k+2}{k+2}$=$\frac{3(k+2)-4}{k+2}$=3-$\frac{4}{k+2}$,
∵y=kx+b(k≠0),且y随x的增大而增大,
∴k>0,
∴-2<-$\frac{4}{k+2}$<0,
∴1<x<3,
即点N的横坐标的取值范围为1<x<3,
故答案为:1<x<3
点评 本题主要考查两函数的交点问题,用k表示出N点的横坐标是解题的关键,注意一次函数的增减性与k的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1. 已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=$\frac{k}{x}$(x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=$\frac{k}{x}$(x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
 已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=$\frac{k}{x}$(x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=$\frac{k}{x}$(x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $-\sqrt{3}$ | C. | -2 | D. | -3 |
5.某人出去散步,从家里出发,走了20min,到达一个离家900m的阅报亭,看了10min报纸后,用了15min返回家里,下面图象中正确表示此人离家的距离y(m)与时间x(min)之家关系的是( )
| A. | 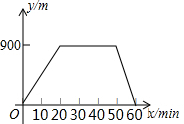 | B. | 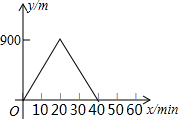 | ||
| C. | 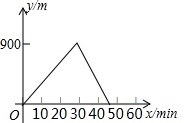 | D. | 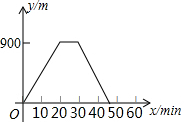 |
2.已知点A、B、C在同一条直线上,线段AB=5,BC=3,则线段AC的长度( )
| A. | 一定是8或2 | B. | 一定是2 | C. | 一定是8 | D. | 以上都不对 |
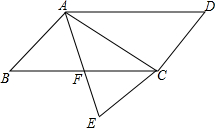 平行四边形ABCD,∠B是锐角,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内点E处.
平行四边形ABCD,∠B是锐角,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内点E处.