题目内容
20.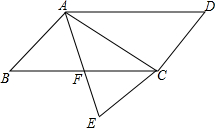 平行四边形ABCD,∠B是锐角,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内点E处.
平行四边形ABCD,∠B是锐角,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内点E处.(1)求证:BF=EF.
(2)如果AE恰好过BC的中点F,连接BE,判断四边形ABEC的形状,说明理由.
分析 (1)由四边形ABCD是平行四边形,得到AD=BC,AD∥BC,于是得到∠DAC=∠ACB,根据将△ACD沿对角线AC折叠得到△ACE,于是得到AE=AD,∠DAC=∠EAC,然后根据等量代换得到结果;
(2)由(1)证得:AF=CF,BF=EF,根据已知条件BF=CF,于是得到BF=AF=CF=EF,即可得到结论.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAC=∠ACB,
∵将△ACD沿对角线AC折叠得到△ACE,
∴AE=AD,∠DAC=∠EAC,
∴∠EAC=∠ACB,
∴AF=CF,
∴BF=BC-CF,EF=AE-AF,
∴BF=EF;
(2)解:四边形ABEC是矩形,
由(1)证得:AF=CF,BF=EF,
∵BF=CF,
∴BF=AF=CF=EF,
∴四边形ABEC是矩形.
点评 本题考查了翻折变换-折叠问题,平行四边形的性质,矩形的判定,熟练掌握折叠的性质是解题的关键.

练习册系列答案
相关题目
13.多项式-a(a-x)(x-b)+ab(a-x)(b-x)的公因式是( )
| A. | -a | B. | -a(a-x)(x-b) | C. | a(a-x) | D. | -a(x-a) |
12.如果两个有理数的和是负数,那么这两个数( )
| A. | 都是正数 | B. | 至少有一个正数 | C. | 都是负数 | D. | 至少有一个负数 |
9.某中学数学兴趣小组12名成员的年龄情况如下:
则这个小组成员年龄的平均数为14,中位数为14,方差为1.5.
| 年龄(岁) | 12 | 13 | 14 | 15 | 16 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
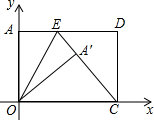 如图,在矩形AOCD中,A(0,15),E在AD上,AE=9,连接CE、OE,将矩形AOCD沿OE折叠,点A恰好落在CE上A′处,求A′的坐标.
如图,在矩形AOCD中,A(0,15),E在AD上,AE=9,连接CE、OE,将矩形AOCD沿OE折叠,点A恰好落在CE上A′处,求A′的坐标.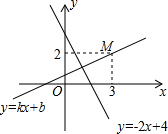 如图,一次函数y=kx+b(k≠0)的图象经过点M(3,2),且与一次函数y=-2x+4的图象交于点N.若对于一次函数y=kx+b(k≠0),当y随x的增大而增大时,则点N的横坐标的取值范围是1<x<3.
如图,一次函数y=kx+b(k≠0)的图象经过点M(3,2),且与一次函数y=-2x+4的图象交于点N.若对于一次函数y=kx+b(k≠0),当y随x的增大而增大时,则点N的横坐标的取值范围是1<x<3.