题目内容
1. 已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=$\frac{k}{x}$(x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=$\frac{k}{x}$(x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $-\sqrt{3}$ | C. | -2 | D. | -3 |
分析 过A作AC垂直于y轴,过B作BD垂直于y轴,易证△AOC∽△OBD,利用反比例函数k的几何意义求出两三角形的面积,得出面积比,在直角三角形AOB中,利用锐角三角函数定义即可求出tan∠B的值,即OA与OB的比值,利用面积比等于相似比的平方,即可求出k值.
解答 解:过A作AC⊥y轴,过B作BD⊥y轴,可得∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,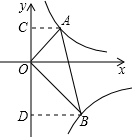
∵OA⊥OB,
∴∠AOC+∠BOD=90°,
∴∠OAC=∠BOD,
∴△AOC∽△OBD,
∵点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=$\frac{k}{x}$(x>0)的图象上,
∴S△AOC=$\frac{1}{2}$,S△OBD=|$\frac{k}{2}$|,
∴S△AOC:S△OBD=1:|k|,
∴($\frac{OA}{OB}$)2=1:|k|,
则在Rt△AOB中,tanB=$\frac{OA}{OB}$=$\frac{\sqrt{3}}{3}$,
∴1:|k|=1:3,
∴|k|=3
∵y=$\frac{k}{x}$(x>0)的图象在第四象限,
∴k=-3.
故选D.
点评 本题考查了相似三角形的判定与性质,锐角三角函数定义,以及反比例函数k的几何意义,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
12.如果两个有理数的和是负数,那么这两个数( )
| A. | 都是正数 | B. | 至少有一个正数 | C. | 都是负数 | D. | 至少有一个负数 |
9.某中学数学兴趣小组12名成员的年龄情况如下:
则这个小组成员年龄的平均数为14,中位数为14,方差为1.5.
| 年龄(岁) | 12 | 13 | 14 | 15 | 16 |
| 人数 | 1 | 4 | 3 | 2 | 2 |
16.要调查下面的问题,适合做普查的是( )
| A. | 某班同学“立定跳远”的成绩 | B. | 某水库中鱼的种类 | ||
| C. | 某鞋厂生产的鞋底承受的弯折次数 | D. | 某型号节能灯的使用寿命 |
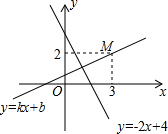 如图,一次函数y=kx+b(k≠0)的图象经过点M(3,2),且与一次函数y=-2x+4的图象交于点N.若对于一次函数y=kx+b(k≠0),当y随x的增大而增大时,则点N的横坐标的取值范围是1<x<3.
如图,一次函数y=kx+b(k≠0)的图象经过点M(3,2),且与一次函数y=-2x+4的图象交于点N.若对于一次函数y=kx+b(k≠0),当y随x的增大而增大时,则点N的横坐标的取值范围是1<x<3.