题目内容
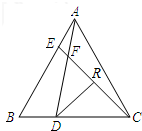 如图,在等边△ABC中,点D、E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
如图,在等边△ABC中,点D、E分别在边BC,AB上,且BD=AE,AD与CE交于点F.(1)求证:AD=CE;
(2)过点D作DR⊥CE于R,求证:DF=2FR.
考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:(1)根据△ABC是等边三角形,得到∠BAC=∠B=60°,AB=AC,再根据AE=BD可以利用SAS证得△AEC≌△BDA,从而证得AD=CE.
(2)根据△AEC≌△BDA得到∠ACE=∠BAD,然后求得∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=60°,通过解该直角三角形证得结论.
(2)根据△AEC≌△BDA得到∠ACE=∠BAD,然后求得∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=60°,通过解该直角三角形证得结论.
解答:(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC
又∵AE=BD
在△AEC与△BDA中,
,
∴△AEC≌△BDA(SAS),
∴AD=CE;
(2)证明:由(1)△AEC≌△BDA,得∠ACE=∠BAD,
∴∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=60°,
∴cos60°=
=
,即DF=2FR.
∴∠BAC=∠B=60°,AB=AC
又∵AE=BD
在△AEC与△BDA中,
|
∴△AEC≌△BDA(SAS),
∴AD=CE;
(2)证明:由(1)△AEC≌△BDA,得∠ACE=∠BAD,
∴∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=60°,
∴cos60°=
| FR |
| DF |
| 1 |
| 2 |
点评:本题考查了等边三角形的性质及全等三角形的判定与性质,解题是关键是发现等边三角形中隐含的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一组数据从小到大排列为2,4,7,x,9,10,若这组数据的中位数为8,则这组数据的众数为( )
| A、7 | B、8 | C、9 | D、10 |
下列各式运算正确的是( )
| A、2a2+3a2=5a4 |
| B、a2•a3•a4=a9 |
| C、2a6÷a3=2a2 |
| D、(a2)3=a5 |
一个钝角三角形的两边长为3、4,则第三边可以为( )
| A、4 | B、5 | C、6 | D、7 |
若M-(-1)2+
=2,则M=( )
| -1×(-1)3-2 |
| 2×(-1)+1 |
| A、-2 | B、-1 | C、1 | D、2 |
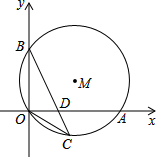 如图,⊙M经过O点,并且与x轴、y轴分别交与A、B两点,线段OA,OB(OA>OB)的长时方程x2-17x+60=0的两根.
如图,⊙M经过O点,并且与x轴、y轴分别交与A、B两点,线段OA,OB(OA>OB)的长时方程x2-17x+60=0的两根.