题目内容
一个圆锥的底面半径为3cm,高位3
cm,求:
(1)圆锥的轴截面中,两母线所夹角(锥角)的度数;
(2)圆锥的全面积;
(3)侧面展开图的圆心角的度数.
| 3 |
(1)圆锥的轴截面中,两母线所夹角(锥角)的度数;
(2)圆锥的全面积;
(3)侧面展开图的圆心角的度数.
考点:圆锥的计算
专题:
分析:(1)如图,△ABC为圆锥的轴截面AO为圆锥的高,OB=OC=3,AO=3
,先利用勾股定理计算出AC=6,则AB=6,则可判断△ABC为等边三角形,所以∠BAC=60°;
(2)根据上题求得的圆锥的母线长后计算出侧面积和底面积即可求得圆锥的全面积;
(3)根据圆锥的底面周长等于圆锥的侧面展开图的弧长,首先求得展开图的弧长,然后根据弧长公式即可求解.
| 3 |
(2)根据上题求得的圆锥的母线长后计算出侧面积和底面积即可求得圆锥的全面积;
(3)根据圆锥的底面周长等于圆锥的侧面展开图的弧长,首先求得展开图的弧长,然后根据弧长公式即可求解.
解答:解:(1)如图,△ABC为圆锥的轴截面, AO为圆锥的高,
AO为圆锥的高,
OB=OC=3,AO=3
,
在Rt△AOC中,AC=
=6,
所以AB=AC=6,
而BC=6,
所以△ABC为等边三角形,
所以∠BAC=60°,
即圆锥轴截面中两母线所夹角的度数为60°.
(2)圆锥的全面积=圆锥的侧面积+圆锥的底面积=π×3×6+π×32=18π+9π=27πcm2;
(3)圆锥侧面展开图的弧长是:2π×3=6π(cm),
设圆心角的度数是n度.则
=6π,
解得:n=180.
 AO为圆锥的高,
AO为圆锥的高,OB=OC=3,AO=3
| 3 |
在Rt△AOC中,AC=
| OC2+AO2 |
所以AB=AC=6,
而BC=6,
所以△ABC为等边三角形,
所以∠BAC=60°,
即圆锥轴截面中两母线所夹角的度数为60°.
(2)圆锥的全面积=圆锥的侧面积+圆锥的底面积=π×3×6+π×32=18π+9π=27πcm2;
(3)圆锥侧面展开图的弧长是:2π×3=6π(cm),
设圆心角的度数是n度.则
| nπ×6 |
| 180 |
解得:n=180.
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
已知关于x的方程x2=
+1的解为x=1,则关于x的不等式
+x2+1>0的解集是( )
| k |
| x |
| k |
| x |
| A、x<0或x>1 |
| B、x<-1或x>0 |
| C、0<x<1 |
| D、-1<x<0 |
直角三角形的两条边长为5和12,它的斜边长为( )
| A、13 | ||
B、
| ||
C、13或
| ||
| D、13或12 |
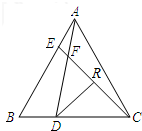 如图,在等边△ABC中,点D、E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
如图,在等边△ABC中,点D、E分别在边BC,AB上,且BD=AE,AD与CE交于点F. a、b、c在数轴上的位置如图所示,求|a+b|-|c-b|的值.
a、b、c在数轴上的位置如图所示,求|a+b|-|c-b|的值. 如图,在正方形网格中,∠AOB的正弦值是
如图,在正方形网格中,∠AOB的正弦值是