题目内容
一个钝角三角形的两边长为3、4，则第三边可以为（ ）
| A、4 | B、5 | C、6 | D、7 |
考点：勾股定理,三角形三边关系
专题：
分析：设第三边为c，根据三角形的三边关系求出c的取值范围，再由三角形是钝角可求得c的最小值即可解题．
解答：解：设第三边为c，
若这个三角形为直角三角形，则第三边为
=5，
∵钝角大于直角，
∴c＞5，
∵三角形第三边小于其余两边和，
∴c＜7，
故选C．
若这个三角形为直角三角形，则第三边为
| 42+32 |
∵钝角大于直角，
∴c＞5，
∵三角形第三边小于其余两边和，
∴c＜7，
故选C．
点评：本题考查了直角三角形中勾股定理的运用，考查了三角形三边关系，本题中根据勾股定理求c＞5是解题的关键．
练习册系列答案
53随堂测系列答案
相关题目
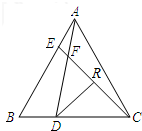如图，在等边△ABC中，点D、E分别在边BC，AB上，且BD=AE，AD与CE交于点F．
a、b、c在数轴上的位置如图所示，求|a+b|-|c-b|的值．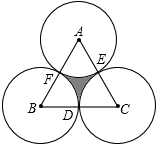
如图，正△ABC的边长为a，D、E、F分别为BC、CA、AB的中点，以A、B、C三点为圆心，直角三角形的两条边长为5和12，它的斜边长为（ ）
| A、13 | ||
B、
| ||
C、13或
| ||
| D、13或12 |