题目内容
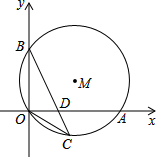 如图,⊙M经过O点,并且与x轴、y轴分别交与A、B两点,线段OA,OB(OA>OB)的长时方程x2-17x+60=0的两根.
如图,⊙M经过O点,并且与x轴、y轴分别交与A、B两点,线段OA,OB(OA>OB)的长时方程x2-17x+60=0的两根.( 1)求线段OA、OB的长;
(2)已知点C在劣弧
 |
| OA |
(3)在(2)的条件下,在⊙M上是否存在一点P,使S△POD=S△ABD?若存在,求出点P的坐标;若不存在,说明理由.
(4)点C在优弧
 |
| OA |
考点:圆的综合题
专题:综合题
分析:(1)利用因式分解法解方程x2-17x+60=0,即可得到OA=12,OB=5;
(2)连结AB、MC、AC,如图1,根据圆周角定理得AB为⊙O的直径,根据勾股定理计算出AB=13,则MC=
,由于OC2=CD•CB,根据相似的判定定理得到△COD∽△CBO,则∠1=∠2,由同弧所对的圆周角相等得到∠2=∠3,所以∠1=∠3,则
=
,根据垂径定理的推论得到MC⊥OA,OH=AH=
OA=6,易得HM=
OB=
,所以CH=CM-HM=4,于是可得C点坐标为(6,-4);
(3)先利用待定系数法确定直线BC的解析式为y=-
x+5,再求出D点坐标为(
,0),则OD=
,AD=OA-OD=
,设P点坐标为(x,y),根据三角形面积公式得到
•
•|y|=
•
•5,解得y=13或-13,利用⊙M的直径为13,可判断⊙M上不存在点P,使其纵坐标为13;
(4)连结AC,CM的延长线交OA于H,如图2,由△COB∽△CDO得到∠4=∠5,利用等角的余角相等得到∠3=∠1,再根据圆内接四边形的性质得∠3=∠2,所以∠1=∠2,于是利用圆周角定理有
=
,然后根据垂径定理的推论得MC⊥OA,OH=AH=
OA=6,加上MH=
,所以CH=CM+MH=9,于是得到C点坐标为(6,9).
(2)连结AB、MC、AC,如图1,根据圆周角定理得AB为⊙O的直径,根据勾股定理计算出AB=13,则MC=
| 13 |
| 2 |
 |
| OC |
 |
| AC |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
(3)先利用待定系数法确定直线BC的解析式为y=-
| 3 |
| 2 |
| 10 |
| 3 |
| 10 |
| 3 |
| 26 |
| 3 |
| 1 |
| 2 |
| 10 |
| 3 |
| 1 |
| 2 |
| 26 |
| 3 |
(4)连结AC,CM的延长线交OA于H,如图2,由△COB∽△CDO得到∠4=∠5,利用等角的余角相等得到∠3=∠1,再根据圆内接四边形的性质得∠3=∠2,所以∠1=∠2,于是利用圆周角定理有
 |
| OC |
 |
| AC |
| 1 |
| 2 |
| 5 |
| 2 |
解答:解:(1)x2-17x+60=0,
(x-12)(x-5)=0,
解得x1=12,x2=5,
所以OA=12,OB=5;
(2)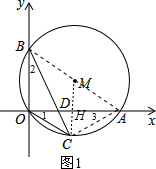 连结AB、MC、AC,MC交OA于H,如图1,
连结AB、MC、AC,MC交OA于H,如图1,
∵∠ACOB=90°,
∴AB为⊙O的直径,AB=
=13,
∴MC=
,
∵OC2=CD•CB,即OC:CD=CB:OC,
而∠OCD=∠BCO,
∴△COD∽△CBO,
∴∠1=∠2,
∵∠2=∠3,
∴∠1=∠3,
∴
=
,
∴MC⊥OA,
∴OH=AH=
OA=6,
∴HM=
OB=
,
∴CH=CM-HM=
-
=4,
∴C点坐标为(6,-4);
(3)不存在.理由如下:
设直线BC的解析式为y=kx+b,
把B(0,5),C(6,-4)代入得
,
解得
,
∴直线BC的解析式为y=-
x+5,
当y=0时,-
x+5=0,解得x=
,
则D点坐标为(
,0),
∴OD=
,AD=OA-OD=
,
∴设P点坐标为(x,y),
∵S△POD=S△ABD,
∴
•
•|y|=
•
•5,解得y=13或-13,
∵⊙M的直径为13,
∴⊙M上不存在点P,使其纵坐标为13;
(4)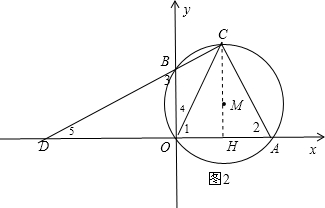 存在.
存在.
连结AC,CM的延长线交OA于H,如图2,
∵△COB∽△CDO,
∴∠4=∠5,
而∠5+∠3=90°,∠4+∠1=90°,
∴∠3=∠1,
∵∠3=∠2,
∴∠1=∠2,
∴
=
,
∴MC⊥OA,
∴OH=AH=
OA=6,
而MH=
,
∴CH=CM+MH=9,
∴C点坐标为(6,9).
(x-12)(x-5)=0,
解得x1=12,x2=5,
所以OA=12,OB=5;
(2)
 连结AB、MC、AC,MC交OA于H,如图1,
连结AB、MC、AC,MC交OA于H,如图1,∵∠ACOB=90°,
∴AB为⊙O的直径,AB=
| OB2+OA2 |
∴MC=
| 13 |
| 2 |
∵OC2=CD•CB,即OC:CD=CB:OC,
而∠OCD=∠BCO,
∴△COD∽△CBO,
∴∠1=∠2,
∵∠2=∠3,
∴∠1=∠3,
∴
 |
| OC |
 |
| AC |
∴MC⊥OA,
∴OH=AH=
| 1 |
| 2 |
∴HM=
| 1 |
| 2 |
| 5 |
| 2 |
∴CH=CM-HM=
| 13 |
| 2 |
| 5 |
| 2 |
∴C点坐标为(6,-4);
(3)不存在.理由如下:
设直线BC的解析式为y=kx+b,
把B(0,5),C(6,-4)代入得
|
解得
|
∴直线BC的解析式为y=-
| 3 |
| 2 |
当y=0时,-
| 3 |
| 2 |
| 10 |
| 3 |
则D点坐标为(
| 10 |
| 3 |
∴OD=
| 10 |
| 3 |
| 26 |
| 3 |
∴设P点坐标为(x,y),
∵S△POD=S△ABD,
∴
| 1 |
| 2 |
| 10 |
| 3 |
| 1 |
| 2 |
| 26 |
| 3 |
∵⊙M的直径为13,
∴⊙M上不存在点P,使其纵坐标为13;
(4)
 存在.
存在.连结AC,CM的延长线交OA于H,如图2,
∵△COB∽△CDO,
∴∠4=∠5,
而∠5+∠3=90°,∠4+∠1=90°,
∴∠3=∠1,
∵∠3=∠2,
∴∠1=∠2,
∴
 |
| OC |
 |
| AC |
∴MC⊥OA,
∴OH=AH=
| 1 |
| 2 |
而MH=
| 5 |
| 2 |
∴CH=CM+MH=9,
∴C点坐标为(6,9).
点评:本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理和相似三角形的判定与性质.会利用待定系数法求一次函数解析式,利用两点间的距离公式计算线段的长;理解坐标与图形性质.

练习册系列答案
相关题目
在-
,
,
,0.3030030003,-
,3.14中,无理数的个数为( )
| π |
| 3 |
| 3 | 64 |
| 7 |
| 22 |
| 7 |
| A、2个 | B、3个 | C、4个 | D、5个 |
 (1)a,b,c在数轴上的位置如图所示,化简|b+a|-|c-b|-2|c-a|.
(1)a,b,c在数轴上的位置如图所示,化简|b+a|-|c-b|-2|c-a|.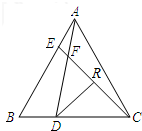 如图,在等边△ABC中,点D、E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
如图,在等边△ABC中,点D、E分别在边BC,AB上,且BD=AE,AD与CE交于点F. 如图,AB是⊙O的直径,CD是切线,AC⊥CD,DE⊥AB,求证:DE2=AC•FC.
如图,AB是⊙O的直径,CD是切线,AC⊥CD,DE⊥AB,求证:DE2=AC•FC.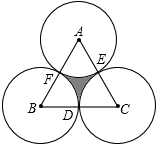 如图,正△ABC的边长为a,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,
如图,正△ABC的边长为a,D、E、F分别为BC、CA、AB的中点,以A、B、C三点为圆心,