题目内容
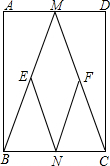 已知如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是BM,CM的中点.
已知如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是BM,CM的中点.(1)判断四边形MENF是什么特殊四边形,并证明你的结论;
(2)当AD=mDC时,四边形MENF是正方形,求m的值.
考点:菱形的判定,全等三角形的判定与性质,正方形的判定
专题:
分析:(1)先根据SAS证明△ABM≌△DCM,得出BM=CM,再根据三角形的中位线定理得出EN=MF,EM=FN,从而根据四条边相等的四边形是菱形得出结论.
(2)可以利用正方形的性质得到MA=AB=MD,从而确定m的值.
(2)可以利用正方形的性质得到MA=AB=MD,从而确定m的值.
解答:解:(1)四边形MENF是菱形,理由如下:
∵四边形ABCD是矩形,
∴AB=CD,∠A=∠D.
∵M是AD的中点,
∴AM=DM.
在△ABM与△DCM中,
,
∴△ABM≌△DCM(SAS),
∴BM=CM.
∵M、N分别是AD、BC的中点,E、F分别是BM、CM的中点,
∴EN=
CM=MF,EM=
BM=FN,
∴ME=EN=NF=FM,
∴四边形MENF是菱形;
(2)当AD=mDC时,四边形MENF是正方形,
∴∠EMF=90°,
由(1)知:Rt△ABM≌Rt△DCM(SAS),
∴∠AMB=∠DMC=45°,
此时MA=MD=DC,
∴AD=2DC,
∴m=2.
∵四边形ABCD是矩形,
∴AB=CD,∠A=∠D.
∵M是AD的中点,
∴AM=DM.
在△ABM与△DCM中,
|
∴△ABM≌△DCM(SAS),
∴BM=CM.
∵M、N分别是AD、BC的中点,E、F分别是BM、CM的中点,
∴EN=
| 1 |
| 2 |
| 1 |
| 2 |
∴ME=EN=NF=FM,
∴四边形MENF是菱形;
(2)当AD=mDC时,四边形MENF是正方形,
∴∠EMF=90°,
由(1)知:Rt△ABM≌Rt△DCM(SAS),
∴∠AMB=∠DMC=45°,
此时MA=MD=DC,
∴AD=2DC,
∴m=2.
点评:本题主要考查了菱形的判定.菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义,②四边相等,③对角线互相垂直平分.

练习册系列答案
相关题目
 如图在直角坐标系中,已知A(0,a),B(b,0)C(3,c)三点,若a,b,c满足关系式:|a-2|+(b-3)2+
如图在直角坐标系中,已知A(0,a),B(b,0)C(3,c)三点,若a,b,c满足关系式:|a-2|+(b-3)2+
 如图,边长为4的正方形AOCD的顶点A、C分别在y轴和x轴上,点P的坐标为(2,0),以点P为圆心,OP的长为半径向正方形内部作一半圆,交线段DF于点F,线段DF的延长线交y轴于点E,DF=DC
如图,边长为4的正方形AOCD的顶点A、C分别在y轴和x轴上,点P的坐标为(2,0),以点P为圆心,OP的长为半径向正方形内部作一半圆,交线段DF于点F,线段DF的延长线交y轴于点E,DF=DC