题目内容
11.若二元一次联立方程式$\left\{\begin{array}{l}{2x+y=14}\\{-3x+2y=21}\end{array}\right.$的解为x=a,y=b,则a+b之值为何?( )| A. | $\frac{19}{2}$ | B. | $\frac{21}{2}$ | C. | 7 | D. | 13 |
分析 将其中一个方程两边乘以一个数,使其与另一方程中x的系数互为相反数,再将两方程相加,消去一个未知数,达到降元的目的,求出另一个未知数,再用代入法求另一个未知数.
解答 解:$\left\{\begin{array}{l}{2x+y=14①}\\{-3x+2y=21②}\end{array}\right.$
①×2-②得,7x=7,
x=1,代入①中得,2+y=14,
解得y=12,
则a+b=1+12=13,
故选D.
点评 本题主要考查解二元一次方程组,熟练运用加减消元是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列运算正确的是( )
| A. | x3+x=2x4 | B. | a2•a3=a6 | C. | (-2x2)3=-8x6 | D. | (x+3y)(x-3y)=x2-3y2 |
16.学考考试报名人数逐年上升,去年约有64000人报考,64000用科学记数法可记作( )
| A. | 64×104 | B. | 6.4×105 | C. | 6.4×104 | D. | 0.64×105 |
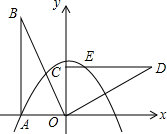 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴上,顶点B的坐标为(-2,4),抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c经过点A,将Rt△OAB绕着点O按顺时针方向旋转90°得到△OCD,点C为点A的对应点,点E为抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c于线段CD的交点.
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴上,顶点B的坐标为(-2,4),抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c经过点A,将Rt△OAB绕着点O按顺时针方向旋转90°得到△OCD,点C为点A的对应点,点E为抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c于线段CD的交点.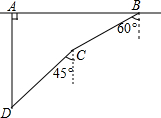 如图,在一次军事演习中,蓝方在一条东西走向的公路上的A 处朝正南方向撤退,红方在公路上的B 处沿南偏西60°方向前进实施拦截.红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方.求红蓝双方最初相距多远(结果不取近似值).
如图,在一次军事演习中,蓝方在一条东西走向的公路上的A 处朝正南方向撤退,红方在公路上的B 处沿南偏西60°方向前进实施拦截.红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方.求红蓝双方最初相距多远(结果不取近似值).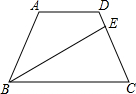 如图,在等腰梯形ABCD中,AD∥BC,AD=1,BC=3,∠ABC的平分线交腰CD于点E(不与点C、D重合).
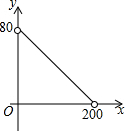
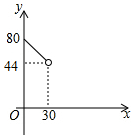
如图,在等腰梯形ABCD中,AD∥BC,AD=1,BC=3,∠ABC的平分线交腰CD于点E(不与点C、D重合).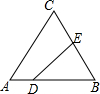 如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )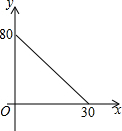

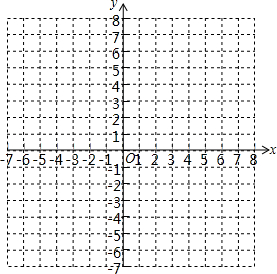 请用学过的方法研究一类新函数y=$\frac{k}{{x}^{2}}$(k为常数,k≠0)的图象和性质.
请用学过的方法研究一类新函数y=$\frac{k}{{x}^{2}}$(k为常数,k≠0)的图象和性质.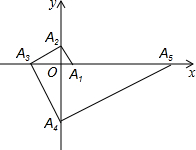 如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为-($\sqrt{3}$)2015.
如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为-($\sqrt{3}$)2015.