题目内容
1.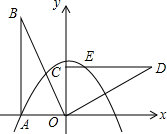 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴上,顶点B的坐标为(-2,4),抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c经过点A,将Rt△OAB绕着点O按顺时针方向旋转90°得到△OCD,点C为点A的对应点,点E为抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c于线段CD的交点.
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴上,顶点B的坐标为(-2,4),抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c经过点A,将Rt△OAB绕着点O按顺时针方向旋转90°得到△OCD,点C为点A的对应点,点E为抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c于线段CD的交点.(1)用含有b的代数式表示c.
(2)若抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c与△OCD的各边共有两个交点,求b的取值范围.
(3)在图中画出点E旋转前的对应点F,连结OF、EF,设由线段OF、FE、ED、DO首尾顺次连结组成的封闭图形的面积为S.
①当直线EF∥OD时,求线段EF的长.
②当S=6时,求抛物线y=-$\frac{1}{2}$x2+bx+c的表达式.
分析 (1)首先由旋转的性质,可求得A(-2,0),C(0,2),D(4,2),然后由抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c经过点A,代入求得答案;
(2)分别求得抛物线y=-$\frac{1}{2}{x}^{2}$+bx+c过原点与过D点时的b的取值,继而求得b的取值范围;
(3)①首先过点E作EH⊥OD,垂足为H,设EH=m,易得△EOF为等腰直角三角形,△EOH为等腰直角三角形,△DEH∽△DOC,则可求得OD=3m,继而求得m的值,则可求得答案;
②首先设E点横坐标为a,易得方程$\frac{1}{2}$(a2+4)+$\frac{1}{2}$×2(4-a)=6,继而求得答案.
解答 解:(1)由题意可得:A(-2,0),C(0,2),D(4,2),
∵抛物线经过点A,
∴-$\frac{1}{2}$×4-2b+c=0,
解得:c=2b+2;
(2)抛物线经过原点,c=0,2b+2=0,
解得:b=-1,
∵抛物线经过点D,则-$\frac{1}{2}$×16+4b+2b+2=2,
解得:b=$\frac{4}{3}$,
∴-1<b<$\frac{4}{3}$;
(3)①过点E作EH⊥OD,垂足为H, 设EH=m,
设EH=m,
∵△EOF为等腰直角三角形,
∴∠FEO=45°,
∵EF∥OD,
∴∠EOD=45°,
在等腰直角△OEH中,EH=OH=m,
∵∠EHD=∠OCD=90°,∠D是公共角,
∴△DEH∽△DOC,
∴EH:DH=OC:CD=2:4,
∴Rt△EDH中,DH=2EH=2m,
∴OD=3m=2$\sqrt{5}$,
∴m=$\frac{2\sqrt{5}}{3}$,
∴EF=$\sqrt{2}$OE=2OH=$\frac{4\sqrt{5}}{3}$;
②设E点横坐标为a,
则S=S△OEF+S△ODE=$\frac{1}{2}$(a2+4)+$\frac{1}{2}$×2(4-a)=$\frac{{a}^{2}+4}{2}$+(4-a)=6,
解得:a=0或2,
∴点E的坐标为:(0,2)或(2,2),
代入抛物线得到:y=-$\frac{1}{2}$x2+2,y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+3.
点评 此题属于二次函数的综合题,考查了待定系数求函数解析式的知识、旋转的性质、等腰直角三角形的性质以及相似三角形的判定与性质等知识.注意根据题意求得点A,C,D的坐标,准确作出辅助线是关键.

 阅读快车系列答案
阅读快车系列答案| A. | a2-6a+9 | B. | a2-3a+9 | C. | a2-9 | D. | a2-6a-9 |
①等腰三角形的底角一定是锐角;
②等腰三角形的内角平分线与此角所对边上的高重合;
③顶角相等的两个等腰三角形的面积相等;
④等腰三角形的一边不可能是另一边的两倍.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | a2+b2 | B. | a2+ab+b2 | C. | a2+2ab+b2 | D. | a2-2ab+b2 |
| A. | $\frac{19}{2}$ | B. | $\frac{21}{2}$ | C. | 7 | D. | 13 |
 如图是一个圆柱体的三视图,由图中数据计算此圆柱体的侧面积为24π.(结果保留π)
如图是一个圆柱体的三视图,由图中数据计算此圆柱体的侧面积为24π.(结果保留π) 如图,在△ABC中,AC的中点为D,BC的中点为E,F是DE的中点,动点G在边AB上,连接GF,延长GF到点H,使HF=GF,连接HD,HE.
如图,在△ABC中,AC的中点为D,BC的中点为E,F是DE的中点,动点G在边AB上,连接GF,延长GF到点H,使HF=GF,连接HD,HE.