题目内容
4.先化简:$\frac{{x}^{2}+1}{{x}^{2}-1}-\frac{x-2}{x-1}÷\frac{x-2}{x}$,请你再选取一个你最喜欢的数代入求值.分析 原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到最简结果,把x=2代入计算即可求出值.
解答 解:原式=$\frac{{x}^{2}+1}{{x}^{2}-1}$-$\frac{x-2}{x-1}$•$\frac{x}{x-2}$=$\frac{{x}^{2}+1}{{x}^{2}-1}$-$\frac{x(x+1)}{{x}^{2}-1}$=$\frac{-(x-1)}{(x+1)(x-1)}$=-$\frac{1}{x+1}$,
当x=2时,原式=-$\frac{1}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.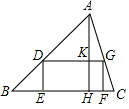 如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
 如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )| A. | 1:1 | B. | 1:2 | C. | 2:3 | D. | $\sqrt{2}$:3 |
13.若圆的半径为5,圆心的坐标是(0,0),点P的坐标是(4,3),则点P与⊙O的位置关系是( )
| A. | 点P在⊙O上 | B. | 点P在⊙O内 | C. | 点P在⊙O外 | D. | 点P不在⊙O上 |
14.在有理数-4,-2,0,3中,大小在-1和2之间的数是( )
| A. | -4 | B. | -2 | C. | 0 | D. | 3 |

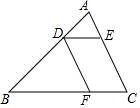 如图,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,则线段BF长为10cm.
如图,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,则线段BF长为10cm.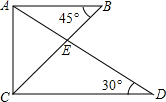 将一副三角尺如图所示叠放在一起,则$\frac{BE}{CE}$的值是$\frac{\sqrt{3}}{3}$.
将一副三角尺如图所示叠放在一起,则$\frac{BE}{CE}$的值是$\frac{\sqrt{3}}{3}$. 如图,在△ABC中,AD是中线,∠B=∠DAC,若BC=8,求AC的长.
如图,在△ABC中,AD是中线,∠B=∠DAC,若BC=8,求AC的长.