题目内容
16. 如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)
如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)
分析 首先构造直角三角形△AEM,利用tan22°=$\frac{AM}{ME}$,求出即可;
解答 解:(1)过点E作EM⊥AB,垂足为M.
设AB为x.
Rt△ABF中,∠AFB=45°,
∴BF=AB=x,
∴BC=BF+FC=x+13,
在Rt△AEM中,∠AEM=22°,AM=AB-BM=AB-CE=x-2,
tan22°=$\frac{AM}{ME}$,
则$\frac{x-2}{x+13}$=$\frac{2}{5}$,
解得:x=12.
即教学楼的高12m.
点评 此题主要考查了解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
8.下列说法正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 四边相等的四边形是菱形 | |
| C. | 一组对边平行的四边形是平行四边形 | |
| D. | 矩形的对角线互相垂直 |
5.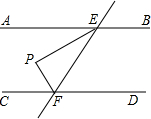 如图,AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作FP⊥EP,若∠PEF=30°,则∠PFC等于( )
如图,AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作FP⊥EP,若∠PEF=30°,则∠PFC等于( )
 如图,AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作FP⊥EP,若∠PEF=30°,则∠PFC等于( )
如图,AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作FP⊥EP,若∠PEF=30°,则∠PFC等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
6.估计-1+$\sqrt{23}$的值( )
| A. | 在4和5之间 | B. | 在3和4之间 | C. | 在2和3之间 | D. | 在1和2之间 |