题目内容
5.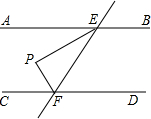 如图,AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作FP⊥EP,若∠PEF=30°,则∠PFC等于( )
如图,AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作FP⊥EP,若∠PEF=30°,则∠PFC等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
分析 根据角平分线定义求出∠AEF,根据平行线的性质求出∠CFE,根据三角形内角和定理求出∠PFE,即可得出答案.
解答 解:∵EP平分∠AEF,∠PEF=30°,
∴∠AEF=2∠PEF=60°,
∵AB∥CD,
∴∠CFE=180°-∠AEF=120°,
∵FP⊥EP,
∴∠P=90°,
∵∠PEF=30°,
∴∠PFE=60°,
∴∠PFC=∠CFE-∠PFE=120°-60°=60°.
故选C.
点评 本题考查了角平分线定义,平行线的性质,三角形内角和定理的应用,主要考查学生运用定理进行推理和计算的能力,题目比较好,难度适中.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
15.下列各数中,最小的是( )
| A. | 3 | B. | $\sqrt{2}$ | C. | -5 | D. | $\frac{π}{3}$ |
10. 如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
 如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
17.若一元二次方程2x2-6x+3=0的两根为x1,x2,则x1x2的值为( )
| A. | 3 | B. | 6 | C. | -6 | D. | $\frac{3}{2}$ |
 如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)
如图,某教学楼AB的后面有一建筑物CD,当光线与地面夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上),求教学楼AB的高度(sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$) 我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75)
我市规划中某地段地铁线路要穿越护城河PQ,站点A和站点B在河的两侧,要测算出A、B间的距离.工程人员在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q出,测得A位于北偏东49°方向,B位于南偏西41°方向.根据以上数据,求A、B间的距离.(参考数据:cos41°≈0.75) 如图是由3个相同的正方体组成的一个立方体图形,它的三视图是( )
如图是由3个相同的正方体组成的一个立方体图形,它的三视图是( )


