题目内容
19.二次函数的y=ax2+bx+c的对称轴在y轴的右侧,且与y轴的交点是P(0,-2),则点A(ab,c)在第三象限.分析 由对称轴判定ab的符号,然后根据抛物线与y轴的交点判断c与0的关系,进而得出结论即可.
解答 解:∵二次函数的y=ax2+bx+c的对称轴在y轴的右侧,
∴对称轴x=-$\frac{b}{2a}$>0,
∴a、b异号,即ab<0.
∵该抛物线与y轴的交点是P(0,-2),
∴c=-2<0,
∴点A(ab,c)位于第三象限.
故答案为:三.
点评 本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列分式中,是最简分式的是( )
| A. | $\frac{x+1}{2(x+1)}$ | B. | $\frac{x-y}{{x}^{2}-{y}^{2}}$ | C. | $\frac{3{x}^{2}+x}{{x}^{2}}$ | D. | $\frac{x+1}{{x}^{2}+1}$ |
9.一个等腰三角形的一边长是7cm,另一边长为5cm,那么这个等腰三角形的周长是( )
| A. | 17cm | B. | 19cm | C. | 17cm或19cm | D. | 12cm |
 如图,方格纸中每个小方格的边长为1个单位长度,△ABC的顶点都在小方格的顶点上,已知点B的坐标是(4,0),点C的坐标是(1,2).
如图,方格纸中每个小方格的边长为1个单位长度,△ABC的顶点都在小方格的顶点上,已知点B的坐标是(4,0),点C的坐标是(1,2).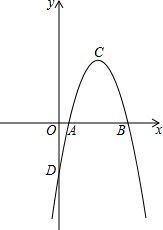 如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A,B两点,交y轴于点D,点C为抛物线的顶点,且A,C两点的横坐标分别为1和4D.
如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A,B两点,交y轴于点D,点C为抛物线的顶点,且A,C两点的横坐标分别为1和4D. 如图,两条直线被三条平行线所截,AB=6,BC=8,DE=4,则DF=$\frac{28}{3}$.
如图,两条直线被三条平行线所截,AB=6,BC=8,DE=4,则DF=$\frac{28}{3}$. 如图,AE交△ABC边BC于点D,∠C=∠E,AD=8,BC=16,若BD:DC=5:3,求DE的长.
如图,AE交△ABC边BC于点D,∠C=∠E,AD=8,BC=16,若BD:DC=5:3,求DE的长.