题目内容
7.【阅读理解】我们知道,1+2+3+…+n=$\frac{n(n+1)}{2}$,那么12+22+32+…+n2结果等于多少呢?
在图1所示三角形数阵中,第1行圆圈中的数为1,即12,第2行两个圆圈中数的和为2+2,即22,…;第n行n个圆圈中数的和为$\underset{\underbrace{n+n+…+n}}{n个n}$,即n2,这样,该三角形数阵中共有$\frac{n(n+1)}{2}$个圆圈,所有圆圈中数的和为12+22+32+…+n2.

【规律探究】
将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n-1行的第一个圆圈中的数分别为n-1,2,n),发现每个位置上三个圆圈中数的和均为2n+1,由此可得,这三个三角形数阵所有圆圈中数的总和为:3(12+22+32+…+n2)=$\frac{n(n+1)(2n+1)}{2}$,因此,12+22+32+…+n2=$\frac{n(n+1)(2n+1)}{6}$.
【解决问题】
根据以上发现,计算:$\frac{{1}^{2}+{2}^{2}+{3}^{2}+…+201{7}^{2}}{1+2+3+…+2017}$的结果为1345.
分析 【规律探究】将同一位置圆圈中的数相加即可,所有圈中的数的和应等于同一位置圆圈中的数的和乘以圆圈个数,据此可得,每个三角形数阵和即为三个三角形数阵和的$\frac{1}{3}$,从而得出答案;
【解决问题】运用以上结论,将原式变形为$\frac{\frac{1}{6}×2017×(2017+1)×(2×2017+1)}{\frac{1}{2}×2017×(2017+1)}$,化简计算即可得.
解答 解:【规律探究】
由题意知,每个位置上三个圆圈中数的和均为n-1+2+n=2n+1,
由此可得,这三个三角形数阵所有圆圈中数的总和为:
3(12+22+32+…+n2)=(2n+1)×(1+2+3+…+n)=(2n+1)×$\frac{n(n+1)}{2}$,
因此,12+22+32+…+n2=$\frac{n(2n+1)(n+1)}{6}$;
故答案为:2n+1,$\frac{n(n+1)(2n+1)}{2}$,$\frac{n(n+1)(2n+1)}{6}$;
【解决问题】
原式=$\frac{\frac{1}{6}×2017×(2017+1)×(2×2017+1)}{\frac{1}{2}×2017×(2017+1)}$=$\frac{1}{3}$×(2017×2+1)=1345,
故答案为:1345.
点评 本题主要考查数字的变化类,阅读材料、理解数列求和的具体方法得出规律,并运用规律解决实际问题是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.公式L=L0+KP表示当重力为P时的物体作用在弹簧上时弹簧的长度,L0代表弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧拉伸的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( )
| A. | L=10+0.5P | B. | L=10+5P | C. | L=80+0.5P | D. | L=80+5P |
15.-52的倒数是( )
| A. | 25 | B. | -25 | C. | $\frac{1}{25}$ | D. | -$\frac{1}{25}$ |
2.|-2017|的相反数是( )
| A. | 2017 | B. | $\frac{1}{2017}$ | C. | -2017 | D. | -$\frac{1}{2017}$ |
12.数据6,8,8,x的众数有两个,则这组数据的中位数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
19.分解因式:x2y-4y结果正确的是( )
| A. | y(x2-4) | B. | y(x-2)2 | C. | y(x+2)2 | D. | y(x+2)(x-2) |
16.下列运算正确的是( )
| A. | $\frac{1}{x}-\frac{1}{y}=\frac{x-y}{xy}$ | B. | $\frac{b}{a-b}$+$\frac{a}{b-a}$=-1 | C. | $\frac{-a-1}{{{a^2}-1}}=-\frac{1}{a+1}$ | D. | $\frac{{{a^2}-1}}{a}•\frac{1}{a+1}=-1$ |
17.已知正比例函数y=3x,若该正比例函数经过点(m,6m-1),则m的值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{2}$ |
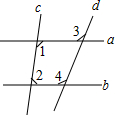 如图,若∠1+∠2=180°,∠3=110°,则∠4=110°.
如图,若∠1+∠2=180°,∠3=110°,则∠4=110°.