题目内容
3. 如图,点P在平行四边形ABCD内,且∠ABP=∠ADP,求证:∠DAP=∠DCP.
如图,点P在平行四边形ABCD内,且∠ABP=∠ADP,求证:∠DAP=∠DCP.
分析 首先过点P作PE∥AD交AB于E,GH∥AB交BC、AD于G、H,可得四边形AEPH、BGPE、CDHG都是平行四边形,易证得∠ABP=∠ADP,∠PEB=∠PHD,即可得△PBE∽△PDH,证得$\frac{PE}{PH}=\frac{BE}{DH}$,然后由平行四边形的对边相等,证得$\frac{PE}{AE}=\frac{PG}{CG}$.又由∠PEA=∠PGC,证得△PAE∽△PCG,继而证得结论.
解答  证明:过点P作PE∥AD交AB于E,GH∥AB交BC、AD于G、H.
证明:过点P作PE∥AD交AB于E,GH∥AB交BC、AD于G、H.
∵四边形ABCD是平行四边形.
∴AD∥BC∥PE,AB∥CD∥GH.
∴∠PEA=∠ABC=∠PGC,∠PEB=∠BAD=∠PHD.
∵∠ABP=∠ADP,∠PEB=∠PHD,
∴△PBE∽△PDH,
∴$\frac{PE}{PH}=\frac{BE}{DH}$,
∵四边形AEPH、BGPE、CDHG都是平行四边形,
∴AE=PH,BE=PG,DH=CG.
∴$\frac{PE}{AE}=\frac{PG}{CG}$.
又∵∠PEA=∠PGC,
∴△PAE∽△PCG.
∴∠BAP=∠BCP,
∵∠BAD=∠BCD,
∴∠DAP=∠DCP.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
13.下列关系中,变量y与x成反比例关系的是( )
| A. | 当电流为定值时,电压y与电阻x | |
| B. | 某销售员计划一个月(30天)销售空调y台,每天销售x台 | |
| C. | 三角形的面积为定值G,一边长为x,这边上的高为y | |
| D. | 汽车在高速公路上匀速行驶,行驶路程y和行驶时间x |
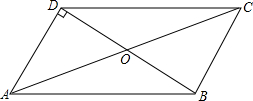 如图,在?ABCD中,AD⊥BD,垂足为D,OA=4,OB=2,求:
如图,在?ABCD中,AD⊥BD,垂足为D,OA=4,OB=2,求: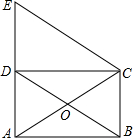 如图,矩形ABCD的对角线AC、BD相交于点O,过点C作BD的平行线与AD的延长线相交于点E.求证:△ACE是等腰三角形.
如图,矩形ABCD的对角线AC、BD相交于点O,过点C作BD的平行线与AD的延长线相交于点E.求证:△ACE是等腰三角形.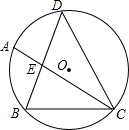 如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E.
如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E.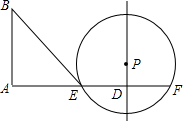 如图,已知线段AD=10,过点D作PD⊥AD于D,点P是直线PD上一点,且PD=3,以点P为圆心,半径为5作⊙P交线段AD于点E及AD的延长线于点F,又过点A作BA⊥AD于A,BA=8,连接BE、PE.
如图,已知线段AD=10,过点D作PD⊥AD于D,点P是直线PD上一点,且PD=3,以点P为圆心,半径为5作⊙P交线段AD于点E及AD的延长线于点F,又过点A作BA⊥AD于A,BA=8,连接BE、PE.